历史
十七世纪 双曲线扇形 是
笛卡尔平面
{
(
x
,
y
)
}
{\displaystyle \{(x,y)\}}
上的一个区域,由从原点到
(
a
,
1
a
)
{\displaystyle (a,{\frac {1}{a}})}
和
(
b
,
1
b
)
{\displaystyle (b,{\frac {1}{b}})}
的射线,以及
双曲线
x
y
=
1
{\displaystyle xy=1}
围成。在标准位置的双曲线扇形有
a
=
1
{\displaystyle a=1}
且
b
>
1
{\displaystyle b>1}
,它的面积为
ln
(
b
)
{\displaystyle \ln(b)}
[2] ,此时双曲线扇形对应正
双曲角 。
当直角双曲线下的两段面积相等时,
x
{\displaystyle x}
的值呈
等比数列 ,
x
2
x
1
=
x
1
x
0
=
k
{\displaystyle {\frac {x_{2}}{x_{1}}}={\frac {x_{1}}{x_{0}}}=k}
,
y
{\displaystyle y}
的值也呈等比数列,
x
2
x
1
=
x
1
x
0
=
1
k
{\displaystyle {\frac {x_{2}}{x_{1}}}={\frac {x_{1}}{x_{0}}}={\frac {1}{k}}}
。
约翰·纳皮尔 在1614年[3] 约斯特·比尔吉 在6年后[4] 对数表 ,当时通过对接近1的底数的大量乘幂 运算,来找到指定范围和精度的对数 和所对应的真数,当时还没出现有理数幂的概念。按后世的观点,约斯特·比尔吉的底数1.000110000 相当接近自然对数的底数
e
{\displaystyle e}
约翰·纳皮尔 的底数0.999999910000000 相当接近
1
e
{\displaystyle {\frac {1}{e}}}
[5] 约翰·纳皮尔 用了20年时间进行相当于数百万次乘法的计算,Henry Briggs [6] 常用对数 表的编制。
形如
f
(
x
)
=
x
p
{\displaystyle f(x)=x^{p}}
反导数 ,除了特殊情况
p
=
−
1
{\displaystyle p=-1}
弓形面积 双曲线扇形 ;其他情况都由1635年发表的卡瓦列里弓形面积公式 [7] 阿基米德 完成(抛物线的弓形面积 Grégoire de Saint-Vincent
x
y
=
1
{\displaystyle xy=1}
[
a
,
b
]
{\displaystyle [a,b]}
双曲线扇形 同
[
c
,
d
]
{\displaystyle [c,d]}
a
b
=
c
d
{\displaystyle {\frac {a}{b}}={\frac {c}{d}}}
x
=
1
{\displaystyle x=1}
x
=
t
{\displaystyle x=t}
f
(
t
)
{\displaystyle f(t)}
[8]
f
(
t
u
)
=
f
(
t
)
+
f
(
u
)
.
{\displaystyle f(tu)=f(t)+f(u).\,}
1649年,Alphonse Antonio de Sarasa 伊萨克·牛顿 推广了二项式定理 ,他将
1
1
+
x
{\displaystyle {\frac {1}{1+x}}}
尼古拉斯·麦卡托 在1668年出版的著作《Logarithmotechnia》中[9] 麦卡托级数 。
十八世纪 大约1730年,欧拉 定义互为逆函数的指数函数 和自然对数为[10] [11]
e
x
=
lim
n
→
∞
(
1
+
x
n
)
n
,
{\displaystyle e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n},}
ln
(
x
)
=
lim
n
→
∞
n
(
x
1
n
−
1
)
{\displaystyle \ln(x)=\lim _{n\rightarrow \infty }n\left(x^{\frac {1}{n}}-1\right)}
1742年威廉·琼斯 发表了现在的幂 指数 概念[12]
形式定义
欧拉 定义自然对数为序列的极限 :
ln
(
x
)
=
lim
n
→
∞
n
(
x
1
n
−
1
)
.
{\displaystyle \ln(x)=\lim _{n\rightarrow \infty }n\left(x^{\frac {1}{n}}-1\right).}
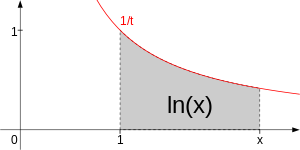
ln
(
a
)
{\displaystyle \ln(a)}
积分 ,
ln
(
a
)
=
∫
1
a
1
x
d
x
.
{\displaystyle \ln(a)=\int _{1}^{a}{\frac {1}{x}}\,dx.}
这个函数为对数是因满足对数 的基本性质:
ln
(
a
b
)
=
ln
(
a
)
+
ln
(
b
)
.
{\displaystyle \ln(ab)=\ln(a)+\ln(b).\,\!}
这可以通过将定义了
ln
(
a
b
)
{\displaystyle \ln(ab)}
换元
x
=
t
a
{\displaystyle x=ta}
ln
(
a
b
)
=
∫
1
a
b
1
x
d
x
=
∫
1
a
1
x
d
x
+
∫
a
a
b
1
x
d
x
=
∫
1
a
1
x
d
x
+
∫
1
b
1
a
t
d
(
a
t
)
{\displaystyle \ln(ab)=\int _{1}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{a}^{ab}{\frac {1}{x}}\;dx=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{at}}\;d(at)}
=
∫
1
a
1
x
d
x
+
∫
1
b
1
t
d
t
=
ln
(
a
)
+
ln
(
b
)
.
{\displaystyle =\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{t}}\;dt=\ln(a)+\ln(b).}
幂公式
ln
(
t
r
)
=
r
ln
(
t
)
{\displaystyle \ln(t^{r})=r\ln(t)}
ln
(
t
r
)
=
∫
1
t
r
1
x
d
x
=
∫
1
t
1
u
r
d
(
u
r
)
=
∫
1
t
1
u
r
(
r
u
r
−
1
d
u
)
=
r
∫
1
t
1
u
d
u
=
r
ln
(
t
)
.
{\displaystyle \ln(t^{r})=\int _{1}^{t^{r}}{\frac {1}{x}}dx=\int _{1}^{t}{\frac {1}{u^{r}}}d\left(u^{r}\right)=\int _{1}^{t}{\frac {1}{u^{r}}}\left(ru^{r-1}\,du\right)=r\int _{1}^{t}{\frac {1}{u}}\,du=r\ln(t).}
第二个等式使用了换元
u
=
x
1
r
{\displaystyle u=x^{\frac {1}{r}}}
自然对数还有在某些情况下更有用的另一个积分表示:
ln
(
x
)
=
−
lim
ϵ
→
0
∫
ϵ
∞
d
t
t
(
e
−
x
t
−
e
−
t
)
.
{\displaystyle \ln(x)=-\lim _{\epsilon \to 0}\int _{\epsilon }^{\infty }{\frac {dt}{t}}\left(e^{-xt}-e^{-t}\right).}
性质
ln
(
1
)
=
∫
1
1
1
t
d
t
=
0
{\displaystyle \ln(1)=\int _{1}^{1}{\frac {1}{t}}\,dt=0\,}
ln
(
−
1
)
=
i
π
{\displaystyle \operatorname {ln} (-1)=i\pi \,}
(参见复数对数 )
ln
(
x
)
<
ln
(
y
)
f
o
r
0
<
x
<
y
{\displaystyle \ln(x)<\ln(y)\quad {\rm {for}}\quad 0<x<y\,}
lim
x
→
0
ln
(
1
+
x
)
x
=
1
{\displaystyle \lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1\,}
ln
(
x
y
)
=
y
ln
(
x
)
{\displaystyle \ln(x^{y})=y\,\ln(x)\,}
x
−
1
x
≤
ln
(
x
)
≤
x
−
1
f
o
r
x
>
0
{\displaystyle {\frac {x-1}{x}}\leq \ln(x)\leq x-1\quad {\rm {for}}\quad x>0\,}
ln
(
1
+
x
α
)
≤
α
x
f
o
r
x
≥
0
,
α
≥
1
{\displaystyle \ln {(1+x^{\alpha })}\leq \alpha x\quad {\rm {for}}\quad x\geq 0,\alpha \geq 1\,}
证明
lim
h
→
0
ln
(
1
+
h
)
h
=
lim
h
→
0
ln
(
1
+
h
)
−
ln
1
h
=
d
d
x
ln
x
|
x
=
1
=
1
{\displaystyle \lim _{h\to 0}{\frac {\ln(1+h)}{h}}=\lim _{h\to 0}{\frac {\ln(1+h)-\ln 1}{h}}={\frac {d}{dx}}\ln x{\Bigg |}_{x=1}=1}
导数
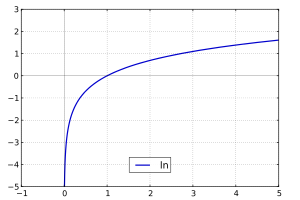
自然对数的图像和它在
x
=
1.5
{\displaystyle x=1.5}
处的切线。
ln
(
1
+
x
)
{\displaystyle \ln(1+x)}
的泰勒多项式只在
−
1
<
x
≤
1
{\displaystyle -1<x\leq 1}
范围内有逐步精确的近似。
自然对数的导数 为
d
d
x
ln
(
x
)
=
1
x
.
{\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}.\,}
证明一 (微积分第一基本定理):
d
d
x
ln
(
x
)
=
d
d
x
∫
1
x
1
t
d
t
=
1
x
{\displaystyle {\frac {d}{dx}}\ln(x)={\frac {d}{dx}}\int _{1}^{x}{\frac {1}{t}}\,dt={\frac {1}{x}}}
证明二: 按此影片 (页面存档备份 ,存于互联网档案馆 )
d
d
x
ln
(
x
)
=
lim
h
→
0
ln
(
x
+
h
)
−
ln
(
x
)
h
{\displaystyle {\frac {d}{dx}}\ln(x)=\lim _{h\to 0}{\frac {\ln(x+h)-\ln(x)}{h}}}
=
lim
h
→
0
ln
(
x
+
h
x
)
h
{\displaystyle =\lim _{h\to 0}{\frac {\ln({\frac {x+h}{x}})}{h}}}
=
lim
h
→
0
[
1
h
ln
(
1
+
h
x
)
]
{\displaystyle =\lim _{h\to 0}\left[{\frac {1}{h}}\ln \left(1+{\frac {h}{x}}\right)\right]\quad }
=
lim
h
→
0
ln
(
1
+
h
x
)
1
h
{\displaystyle =\lim _{h\to 0}\ln \left(1+{\frac {h}{x}}\right)^{\frac {1}{h}}}
设
u
=
h
x
⇒
u
x
=
h
{\displaystyle u={\frac {h}{x}}\Rightarrow ux=h}
1
h
=
1
u
x
{\displaystyle {\frac {1}{h}}={\frac {1}{ux}}}
d
d
x
ln
(
x
)
=
lim
u
→
0
ln
(
1
+
u
)
1
u
x
{\displaystyle {\frac {d}{dx}}\ln(x)=\lim _{u\to 0}\ln(1+u)^{\frac {1}{ux}}}
=
lim
u
→
0
ln
[
(
1
+
u
)
1
u
]
1
x
{\displaystyle =\lim _{u\to 0}\ln \left[(1+u)^{\frac {1}{u}}\right]^{\frac {1}{x}}}
=
1
x
lim
u
→
0
ln
(
1
+
u
)
1
u
{\displaystyle ={\frac {1}{x}}\lim _{u\to 0}\ln(1+u)^{\frac {1}{u}}}
设
n
=
1
u
⇒
u
=
1
n
{\displaystyle n={\frac {1}{u}}\Rightarrow u={\frac {1}{n}}}
d
d
x
ln
(
x
)
=
1
x
lim
n
→
∞
ln
(
1
+
1
n
)
n
{\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}\lim _{n\to \infty }\ln \left(1+{\frac {1}{n}}\right)^{n}}
=
1
x
ln
[
lim
n
→
∞
(
1
+
1
n
)
n
]
{\displaystyle ={\frac {1}{x}}\ln \left[\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\right]}
=
1
x
ln
e
{\displaystyle ={\frac {1}{x}}\ln e}
=
1
x
{\displaystyle ={\frac {1}{x}}}
用自然对数定义的更一般的对数函数,
log
b
(
x
)
=
ln
(
x
)
ln
(
b
)
{\displaystyle \log _{b}(x)={\frac {\ln(x)}{\ln(b)}}}
逆函数 即一般指数函数 的性质,它的导数为[13] [14]
d
d
x
log
b
(
x
)
=
1
x
ln
(
b
)
.
{\displaystyle {\frac {d}{dx}}\log _{b}(x)={\frac {1}{x\ln(b)}}.}
根据链式法则 ,以
f
(
x
)
{\displaystyle f(x)}
d
d
x
ln
[
f
(
x
)
]
=
f
′
(
x
)
f
(
x
)
.
{\displaystyle {\frac {d}{dx}}\ln[f(x)]={\frac {f'(x)}{f(x)}}.}
右手端的商叫做
f
{\displaystyle f}
对数导数
ln
(
f
(
x
)
)
{\displaystyle \ln(f(x))}
f
′
(
x
)
{\displaystyle f'(x)}
对数微分 [15]
幂级数
自然对数的导数性质导致了
ln
(
1
+
x
)
{\displaystyle \ln(1+x)}
泰勒级数 ,也叫做麦卡托级数 :
ln
(
1
+
x
)
=
∑
n
=
1
∞
(
−
1
)
n
+
1
n
x
n
=
x
−
x
2
2
+
x
3
3
−
⋯
{\displaystyle \ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots }
对于所有
|
x
|
≤
1
,
{\displaystyle \left|x\right|\leq 1,}
x
=
−
1.
{\displaystyle x=-1.}
把
x
−
1
{\displaystyle x-1}
x
{\displaystyle x}
ln
(
x
)
{\displaystyle \ln(x)}
欧拉变换 ,可以得到对绝对值大于1的任何
x
{\displaystyle x}
ln
x
x
−
1
=
∑
n
=
1
∞
1
n
x
n
=
1
x
+
1
2
x
2
+
1
3
x
3
+
⋯
.
{\displaystyle \ln {x \over {x-1}}=\sum _{n=1}^{\infty }{1 \over {nx^{n}}}={1 \over x}+{1 \over {2x^{2}}}+{1 \over {3x^{3}}}+\cdots \,.}
这个级数类似于贝利-波尔温-普劳夫公式 。
还要注意到
x
x
−
1
{\displaystyle x \over {x-1}}
y
{\displaystyle y}
x
x
−
1
{\displaystyle x \over {x-1}}
x
{\displaystyle x}
ln
x
=
∑
n
=
1
∞
1
n
(
x
−
1
x
)
n
=
(
x
−
1
x
)
+
1
2
(
x
−
1
x
)
2
+
1
3
(
x
−
1
x
)
3
+
⋯
{\displaystyle \ln {x}=\sum _{n=1}^{\infty }{1 \over {n}}\left({x-1 \over x}\right)^{n}=\left({x-1 \over x}\right)+{1 \over 2}\left({x-1 \over x}\right)^{2}+{1 \over 3}\left({x-1 \over x}\right)^{3}+\cdots \,}
对于
Re
(
x
)
≥
1
2
.
{\displaystyle \operatorname {Re} (x)\geq {\frac {1}{2}}\,.}
自然数的倒数的总和
1
+
1
2
+
1
3
+
⋯
+
1
n
=
∑
k
=
1
n
1
k
,
{\displaystyle 1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots +{\frac {1}{n}}=\sum _{k=1}^{n}{\frac {1}{k}},}
叫做调和级数 。它与自然对数有密切联系:当
n
{\displaystyle n}
∑
k
=
1
n
1
k
−
ln
(
n
)
,
{\displaystyle \sum _{k=1}^{n}{\frac {1}{k}}-\ln(n),}
收敛 于欧拉-马歇罗尼常数 。这个关系有助于分析算法比如快速排序 的性能。[16]
积分
自然对数通过分部积分法 积分:
∫
ln
(
x
)
d
x
=
x
ln
(
x
)
−
x
+
C
.
{\displaystyle \int \ln(x)\,dx=x\ln(x)-x+C.}
假设:
u
=
ln
(
x
)
⇒
d
u
=
d
x
x
{\displaystyle u=\ln(x)\Rightarrow du={\frac {dx}{x}}}
d
v
=
d
x
⇒
v
=
x
{\displaystyle dv=dx\Rightarrow v=x\,}
所以:
∫
ln
(
x
)
d
x
=
x
ln
(
x
)
−
∫
x
x
d
x
=
x
ln
(
x
)
−
∫
1
d
x
=
x
ln
(
x
)
−
x
+
C
{\displaystyle {\begin{aligned}\int \ln(x)\,dx&=x\ln(x)-\int {\frac {x}{x}}\,dx\\&=x\ln(x)-\int 1\,dx\\&=x\ln(x)-x+C\end{aligned}}}
自然对数可以简化形如
g
(
x
)
=
f
′
(
x
)
f
(
x
)
{\displaystyle g(x)={\frac {f'(x)}{f(x)}}}
g
(
x
)
{\displaystyle g(x)}
原函数 给出为
ln
(
|
f
(
x
)
|
)
{\displaystyle \ln(\left\vert f(x)\right\vert )}
链式法则 和如下事实:
d
d
x
ln
|
x
|
=
1
x
.
{\displaystyle \ {d \over dx}\ln \left|x\right|={1 \over x}.}
换句话说,
∫
1
x
d
x
=
ln
|
x
|
+
C
{\displaystyle \int {1 \over x}dx=\ln |x|+C}
且
∫
f
′
(
x
)
f
(
x
)
d
x
=
ln
|
f
(
x
)
|
+
C
.
{\displaystyle \int {{\frac {f'(x)}{f(x)}}\,dx}=\ln |f(x)|+C.}
例子 下面是
g
(
x
)
=
tan
x
{\displaystyle g(x)=\tan x}
∫
tan
x
d
x
=
∫
sin
x
cos
x
d
x
=
∫
−
d
d
x
cos
x
cos
x
d
x
.
{\displaystyle {\begin{aligned}\int \tan x\,dx&=\int {\sin x \over \cos x}\,dx\\&=\int {-{d \over dx}\cos x \over {\cos x}}\,dx.\\\end{aligned}}}
设
f
(
x
)
=
cos
x
{\displaystyle f(x)=\cos x}
f
′
(
x
)
=
−
sin
x
{\displaystyle f'(x)=-\sin x}
∫
tan
x
d
x
=
−
ln
|
cos
x
|
+
C
=
ln
|
sec
x
|
+
C
{\displaystyle {\begin{aligned}\int \tan x\,dx&=-\ln {\left|\cos x\right|}+C\\&=\ln {\left|\sec x\right|}+C\\\end{aligned}}}
与双曲函数的关系
在
直角双曲线 (方程
y
=
1
x
{\displaystyle y={\frac {1}{x}}}
)下,双曲线三角形(黄色),和对应于
双曲角
u
{\displaystyle u}
的
双曲线扇形 (红色)。这个三角形的边分别是
双曲函数 中
cosh
{\displaystyle \cosh }
和
sinh
{\displaystyle \sinh }
的
2
{\displaystyle {\sqrt {2}}}
倍。
射线出原点交
单位双曲线
x
2
−
y
2
=
1
{\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}
于点
(
cosh
a
,
sinh
a
)
{\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}
,这里的
a
{\displaystyle \scriptstyle a}
是射线、双曲线和
x
{\displaystyle \scriptstyle x}
轴围成的面积的二倍。对于双曲线上位于x轴下方的点,这个面积被认为是负值。
在18世纪,约翰·海因里希·兰伯特 介入双曲函数 [17] 双曲几何 中双曲三角形 的面积[18] 直角双曲线
x
y
=
1
{\displaystyle xy=1}
y
=
x
{\displaystyle y=x}
指数函数 ,即要形成指定双曲角
u
{\displaystyle u}
x
{\displaystyle x}
y
{\displaystyle y}
(
e
u
+
e
−
u
)
2
2
{\displaystyle \left(e^{u}+e^{-u}\right){\frac {\sqrt {2}}{2}}}
(
e
u
−
e
−
u
)
2
2
{\displaystyle \left(e^{u}-e^{-u}\right){\frac {\sqrt {2}}{2}}}
通过旋转和缩小线性变换 ,得到单位双曲线 下的情况,有:
cosh
x
=
e
x
+
e
−
x
2
{\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}}}
sinh
x
=
e
x
−
e
−
x
2
{\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}}}
单位双曲线 中双曲线扇形的面积是对应直角双曲线
x
y
=
1
{\displaystyle xy=1}
1
2
{\displaystyle {\frac {1}{2}}}
连分数
尽管自然对数没有简单的连分数 ,但有一些广义连分数 如:
ln
(
1
+
x
)
=
x
1
1
−
x
2
2
+
x
3
3
−
x
4
4
+
x
5
5
−
⋯
=
x
1
−
0
x
+
1
2
x
2
−
1
x
+
2
2
x
3
−
2
x
+
3
2
x
4
−
3
x
+
4
2
x
5
−
4
x
+
⋱
{\displaystyle {\begin{aligned}\ln(1+x)&={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\cdots \\&={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}\\\end{aligned}}}
ln
(
1
+
x
y
)
=
x
y
+
1
x
2
+
1
x
3
y
+
2
x
2
+
2
x
5
y
+
3
x
2
+
⋱
=
2
x
2
y
+
x
−
(
1
x
)
2
3
(
2
y
+
x
)
−
(
2
x
)
2
5
(
2
y
+
x
)
−
(
3
x
)
2
7
(
2
y
+
x
)
−
⋱
{\displaystyle {\begin{aligned}\ln \left(1+{\frac {x}{y}}\right)&={\cfrac {x}{y+{\cfrac {1x}{2+{\cfrac {1x}{3y+{\cfrac {2x}{2+{\cfrac {2x}{5y+{\cfrac {3x}{2+\ddots }}}}}}}}}}}}\\&={\cfrac {2x}{2y+x-{\cfrac {(1x)^{2}}{3(2y+x)-{\cfrac {(2x)^{2}}{5(2y+x)-{\cfrac {(3x)^{2}}{7(2y+x)-\ddots }}}}}}}}\\\end{aligned}}}
这些连分数特别是最后一个对接近1的值快速收敛。但是,更大的数的自然对数,可以轻易的用这些更小的数的自然对数的加法来计算,带有类似的快速收敛。
例如,因为
2
=
1.25
3
×
1.024
{\displaystyle 2=1.25^{3}\times 1.024}
2的自然对数 可以计算为:
ln
2
=
3
ln
(
1
+
1
4
)
+
ln
(
1
+
3
125
)
=
6
9
−
1
2
27
−
2
2
45
−
3
2
63
−
⋱
+
6
253
−
3
2
759
−
6
2
1265
−
9
2
1771
−
⋱
.
{\displaystyle {\begin{aligned}\ln 2&=3\ln \left(1+{\frac {1}{4}}\right)+\ln \left(1+{\frac {3}{125}}\right)\\&={\cfrac {6}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {6}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\\\end{aligned}}}
进而,因为
10
=
1.25
10
×
1.024
3
{\displaystyle 10=1.25^{10}\times 1.024^{3}}
ln
10
=
10
ln
(
1
+
1
4
)
+
3
ln
(
1
+
3
125
)
=
20
9
−
1
2
27
−
2
2
45
−
3
2
63
−
⋱
+
18
253
−
3
2
759
−
6
2
1265
−
9
2
1771
−
⋱
.
{\displaystyle {\begin{aligned}\ln 10&=10\ln \left(1+{\frac {1}{4}}\right)+3\ln \left(1+{\frac {3}{125}}\right)\\&={\cfrac {20}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {18}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.\\\end{aligned}}}
复数对数
主条目:复数对数
指数函数 可以扩展为对任何复数
x
{\displaystyle x}
e
x
{\displaystyle e^{x}}
x
{\displaystyle x}
x
{\displaystyle x}
e
x
=
0
{\displaystyle e^{x}=0}
e
2
π
i
=
1
=
e
0
{\displaystyle e^{2\pi i}=1=e^{0}}
e
z
=
e
z
+
2
n
π
i
{\displaystyle e^{z}=e^{z+2n\pi i}}
z
{\displaystyle z}
n
{\displaystyle n}
所以对数不能定义在整个复平面 上,并且它是多值函数 ,就是说任何复数对数都可以增加
2
π
i
{\displaystyle 2\pi i}
切割平面 上是单值函数。例如,
log
i
=
1
2
π
i
{\displaystyle \log i={\frac {1}{2}}\pi i}
5
2
π
i
{\displaystyle {\frac {5}{2}}\pi i}
−
3
2
π
i
{\displaystyle -{\frac {3}{2}}\pi i}
i
4
=
1
{\displaystyle i^{4}=1}
4
log
=
i
{\displaystyle 4\log =i}
2
π
i
{\displaystyle 2\pi i}
10
π
i
{\displaystyle 10\pi i}
−
6
π
i
{\displaystyle -6\pi i}
主值定义 对于每个非0复数
z
=
x
+
y
i
{\displaystyle z=x+yi}
log
z
{\displaystyle \log z}
(
−
π
,
π
]
{\displaystyle (-\pi ,\pi ]}
log
0
{\displaystyle \log 0}
w
{\displaystyle w}
e
w
=
0
{\displaystyle e^{w}=0}
要对
log
z
{\displaystyle \log z}
z
{\displaystyle z}
极坐标 形式,
z
=
r
e
i
θ
{\displaystyle z=re^{i\theta }}
z
{\displaystyle z}
θ
{\displaystyle \theta }
2
π
{\displaystyle 2\pi }
θ
{\displaystyle \theta }
(
−
π
,
π
]
{\displaystyle (-\pi ,\pi ]}
θ
{\displaystyle \theta }
arg
z
{\displaystyle \operatorname {arg} z}
atan
2
(
y
,
x
)
{\displaystyle \operatorname {atan} 2(y,x)}
[19]
Log
z
:=
ln
r
+
i
θ
=
ln
|
z
|
+
i
Arg
z
=
ln
x
2
+
y
2
+
i
atan2
(
y
,
x
)
.
{\displaystyle \operatorname {Log} z:={\text{ln }}r+i\theta =\ln |z|+i\operatorname {Arg} z=\operatorname {ln} {\sqrt {x^{2}+y^{2}}}+i\operatorname {atan2} (y,x).}
例如,
Log
(
−
3
i
)
=
ln
3
−
π
i
2
{\displaystyle \operatorname {Log} (-3i)=\ln 3-{\frac {\pi i}{2}}}
常见科学用法
自然指数有应用于表达放射衰变(放射性 )之类关于衰减的过程,如放射性原子数目
N
{\displaystyle N}
d
N
d
t
=
−
p
N
{\displaystyle {\frac {dN}{dt}}=-pN}
p
{\displaystyle p}
N
(
t
)
=
N
(
0
)
exp
(
−
p
t
)
{\displaystyle N(t)=N(0)\exp(-pt)}
注释 参考资料
^ 例如哈代 和赖特 所著的《数论入门》"Introduction to the theory of numbers" (1.7, Sixth edition, Oxford 2008)的注解 "log x is, of course the 'Napierian' logarithm of x, to base e. 'Common' logarithms have no mathematical interest."(log x 当然是以e为基,x的“纳皮尔 ”对数。“常用”对数在数学上毫无重要。)
^ 证明:从1到b 积分1/x ,增加三角形{(0, 0), (1, 0), (1, 1)},并减去三角形{(0, 0), (b , 0), (b , 1/b )}。
^ Ernest William Hobson, John Napier and the invention of logarithms, 1614 , Cambridge: The University Press, 1914 ^ Boyer, Carl B. , 14,Section "Jobst Bürgi" , A History of Mathematics, New York: John Wiley & Sons , 1991, ISBN 978-0-471-54397-8 ^ 选取接近e的底数b,对数表涉及的bx 为单调增函数,定义域为0到1而值域为1到b;选取接近1/e的底数b,对数表涉及的bx 为单调减函数,定义域为0到∞而值域为1到0。
^ 以
10
1
2
54
{\displaystyle 10^{\frac {1}{2^{54}}}}
^ 博纳文图拉·卡瓦列里 在1635年的《Geometria indivisibilibus continuorum nova quadam ratione promota》中给出定积分 :
∫
0
a
x
n
d
x
=
1
n
+
1
a
n
+
1
n
≥
0
,
{\displaystyle \int _{0}^{a}x^{n}\,dx={\tfrac {1}{n+1}}\,a^{n+1}\qquad n\geq 0,}
不定积分 形式为:
∫
x
n
d
x
=
1
n
+
1
x
n
+
1
+
C
n
≠
−
1.
{\displaystyle \int x^{n}\,dx={\tfrac {1}{n+1}}\,x^{n+1}+C\qquad n\neq -1.}
皮埃尔·德·费马 、Gilles de Roberval 埃万杰利斯塔·托里拆利 。^ 设a=1,x轴上[a,b]两点对应的双曲线线段与原点围成的双曲线扇形 面积为f(b),[c,d]对应的扇形面积为f(d)-f(c),d=bc,即为f(bc)-f(c),当且仅当f(bc)=f(b)+f(c)时,两双曲线扇形面积相等。
^ J. J. O'Connor; E. F. Robertson, The number e , The MacTutor History of Mathematics archive, September 2001 [2009-02-02 ] , (原始内容 存档于2012-02-19) ^
卡瓦列里弓形面积公式,对于负数值的n (x 的负数幂),由于在x = 0处有个奇点 ,因此定积分的下限为1,而不是0,即为:
∫
1
a
x
n
d
x
=
1
n
+
1
(
a
n
+
1
−
1
)
n
≠
−
1.
{\displaystyle \int _{1}^{a}x^{n}\,dx={\tfrac {1}{n+1}}(a^{n+1}-1)\qquad n\neq -1.}
欧拉 的自然对数定义:
ln
(
x
)
=
lim
n
→
∞
n
(
x
1
/
n
−
1
)
=
lim
n
→
−
1
1
n
+
1
(
x
n
+
1
−
1
)
.
{\displaystyle {\begin{aligned}\ln(x)&=\lim _{n\rightarrow \infty }n(x^{1/n}-1)\\&=\lim _{n\rightarrow -1}{\tfrac {1}{n+1}}(x^{n+1}-1).\\\end{aligned}}}
^ Maor, Eli, e: The Story of a Number, Princeton University Press , 2009, ISBN 978-0-691-14134-3 Eves, Howard Whitley , An introduction to the history of mathematics, The Saunders series 6th, Philadelphia: Saunders, 1992, ISBN 978-0-03-029558-4 Boyer, Carl B. , A History of Mathematics, New York: John Wiley & Sons , 1991, ISBN 978-0-471-54397-8 ^
(
1
+
1
n
)
x
=
(
(
1
+
1
n
)
n
)
x
n
{\displaystyle \left(1+{\frac {1}{n}}\right)^{x}=\left(\left(1+{\frac {1}{n}}\right)^{n}\right)^{\frac {x}{n}}}
^ Lang 1997 , section IV.2 ^ Wolfram, Stephen . " Calculation of d/dx(Log(b,x)) "Wolfram Alpha : Computational Knowledge Engine, Wolfram Research . (原始内容 存档于2011-07-18) (英语) . ^ Kline, Morris , Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications , 1998, ISBN 978-0-486-40453-0 ^ Havil, Julian, Gamma: Exploring Euler's Constant, Princeton University Press , 2003, ISBN 978-0-691-09983-5 ^ Eves, Howard, Foundations and Fundamental Concepts of Mathematics , Courier Dover Publications: 59, 2012, ISBN 9780486132204We also owe to Lambert the first systematic development of the theory of hyperbolic functions and, indeed, our present notation for these functions. ^ Ratcliffe, John, Foundations of Hyperbolic Manifolds , Graduate Texts in Mathematics 149 , Springer: 99, 2006 [2014-03-28 ] , ISBN 9780387331973原始内容 存档于2014-01-12), That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien , which was published posthumously in 1786. ^ Sarason, Section IV.9.
延伸阅读
John B. Conway, Functions of one complex variable , 2nd edition, Springer, 1978.
Serge Lang , Complex analysis , 3rd edition, Springer-Verlag, 1993.Gino Moretti, Functions of a Complex Variable , Prentice-Hall, Inc., 1964.
Donald Sarason, Complex function theory (页面存档备份 ,存于互联网档案馆 )
E. T. Whittaker and G. N. Watson , A Course in Modern Analysis , fourth edition, Cambridge University Press, 1927.