在数学中,双曲函数是一类与常见的三角函数(也叫圆函数)类似的函数。最基本的双曲函数是双曲正弦函数 和双曲余弦函数
和双曲余弦函数 ,从它们可以导出双曲正切函数
,从它们可以导出双曲正切函数 等,其推导也类似于三角函数的推导。双曲函数的反函数称为反双曲函数。
等,其推导也类似于三角函数的推导。双曲函数的反函数称为反双曲函数。
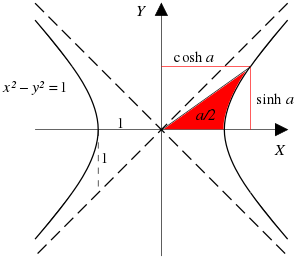
射线出原点交单位双曲线

于点

,这里的

是射线、双曲线和x轴围成的面积的二倍。对于双曲线上位于x轴下方的点,这个面积被认为是负值
双曲函数的定义域是实数,其自变量的值叫做双曲角。双曲函数出现于某些重要的线性微分方程的解中,譬如说定义悬链线和拉普拉斯方程。
基本定义
最简单的几种双曲函数为[1]:
- 双曲正弦:
-
- 双曲余弦:
-
- 双曲正切:
-
- 双曲余切:当
-
- 双曲正割:
-
- 双曲余割:当
-
函数 是关于y轴对称的偶函数。函数 是奇函数。
如同当 遍历实数集 时,点( , )的轨迹是一个圆 一样,当 遍历实数集 时,点( , )的轨迹是单位双曲线 的右半边。这是因为有以下的恒等式:
-
参数t不是圆角而是双曲角,它表示在x轴和连接原点和双曲线上的点( , )的直线之间的面积的两倍。
历史
在
直角双曲线(方程
)下,双曲线三角形(黄色),和对应于
双曲角u的
双曲线扇形(红色)。这个三角形的边分别是
双曲函数中
和
的
倍。
在18世纪,约翰·海因里希·兰伯特引入双曲函数[2],并计算了双曲几何中双曲三角形的面积[3]。自然对数函数是在直角双曲线 下定义的,可构造双曲线直角三角形,底边在线 上,一个顶点是原点,另一个顶点在双曲线。这里以自然对数即双曲角作为参数的函数,是自然对数的逆函数指数函数,即要形成指定双曲角 ,在渐近线即x或y轴上需要有的 或 的值。显见这里的底边是 ,垂线是 。
通过旋转和缩小线性变换,得到单位双曲线下的情况,有:
-
-
单位双曲线中双曲线扇形的面积是对应直角双曲线 下双曲角的 。
虚数圆角定义
双曲角经常定义得如同虚数圆角。实际上,如果 是实数而 ,则
-
所以双曲函数 和 可以通过圆函数来定义。这些恒等式不是从圆或旋转得来的,它们应当以无穷级数的方式来理解。特别是,可以将指数函数表达为由偶次项和奇次项组成,前者形成 函数,后者形成了 函数。 函数的无穷级数可从 得出,通过把它变为交错级数,而 函数可来自将 变为交错级数。上面的恒等式使用虚数 ,从三角函数的级数的项中去掉交错因子 ,来恢复为指数函数的那两部分级数。
-
-
双曲函数可以通过虚数圆角定义为:
- 双曲正弦:[1]
-
- 双曲余弦:[1]
-
- 双曲正切:
-
- 双曲余切:
-
- 双曲正割:
-
- 双曲余割:
-
这些复数形式的定义得出自欧拉公式。
与三角函数的类比
奥古斯都·德·摩根在其1849年出版的教科书《Trigonometry and Double Algebra》中将圆三角学扩展到了双曲线[4]。威廉·金顿·克利福德在1878年使用双曲角来参数化单位双曲线。
给定相同的角α,在双曲线上计算双曲角的量值(双曲扇形面积除以半径)得到双曲函数,角 得到三角函数。在单位圆和单位双曲线上,双曲函数与三角函数有如下的关系:
- 正弦同样是从x轴到曲线的半弦。
- 余弦同样是从y轴到曲线的半弦(图中的余弦是长方形的另一条边)。
- 正切同样是过x轴上单位点(1,0)在曲线上的切线到终边的长度。
- 余切同样是从y轴与过终边和曲线交点的切线与y轴的交点和曲线连线之长度。
- 正割同样是在一个有正切和单位长的直角三角形上,但边不一样。
- 余割同样是y轴与过终边和曲线交点的切线与y轴的交点和原点之距离。
- 角的量值可以从0到无限大,但 实际上只会介于 到 (360度)之间,其余是 的同界角,再绕着圆旋转,故三角函数可以有周期。双曲角的量值可以从 到无限大,但 实际上不会超过 (45度),故无法如三角函数一样有周期性。
恒等式
与双曲函数有关的恒等式如下:
-
-
-
-
-
-
-
-
由于双曲函数和三角函数之间的对应关系,双曲函数的恒等式和三角函数的恒等式之间也是一一对应的。对于一个已知的三角函数公式,只需要将其中的三角函数转成相应的双曲函数,并将含有有两个 的积的项(包括 )转换正负号,就可得到相应的双曲函数恒等式[5]。如
- 三角函数的三倍角公式为:
-
-
- 而对应的双曲函数三倍角公式则是:
-
-
- 三角函数的差角公式为:
- 而对应的双曲函数的差角公式则是:
双曲函数的导数
-
-
-
双曲函数的泰勒展开式
双曲函数也可以以泰勒级数展开:
-
-
-
- (罗朗级数)
-
- (罗朗级数)
其中
- 是第 项伯努利数
- 是第 项欧拉数
双曲函数的积分
-
-
-
-
-
-
与指数函数的关系
从双曲正弦和余弦的定义,可以得出如下恒等式:
-
和
-
复数的双曲函数
因为指数函数可以定义为任何复数参数,也可以扩展双曲函数的定义为复数参数。函数 和 是全纯函数。
指数函数与三角函数的关系由欧拉公式给出:
-
所以:
-
-
-
因此,双曲函数是关于虚部有周期的,周期为 (对双曲正切和余切是 )。
反双曲函数
反双曲函数是双曲函数的反函数。它们的定义为:
-
参考文献
- ^ 1.0 1.1 1.2 Weisstein, Eric W. (编). Hyperbolic Functions. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2020-08-29]. (原始内容存档于2022-05-21) (英语).
- ^ Eves, Howard, Foundations and Fundamental Concepts of Mathematics, Courier Dover Publications: 59, 2012, ISBN 9780486132204,
We also owe to Lambert the first systematic development of the theory of hyperbolic functions and, indeed, our present notation for these functions.
- ^ Ratcliffe, John, Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics 149, Springer: 99, 2006 [2014-03-27], ISBN 9780387331973, (原始内容存档于2014-01-12),
That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786.
- ^ Augustus De Morgan (1849) Trigonometry and Double Algebra (页面存档备份,存于互联网档案馆), Chapter VI: "On the connection of common and hyperbolic trigonometry"
- ^ G. Osborn, Mnemonic for hyperbolic formulae[失效链接], The Mathematical Gazette, p. 189, volume 2, issue 34, July 1902
参见






