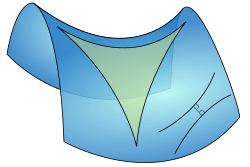
双曲三角形
在双曲几何学中,双曲三角形是指位于双曲面上的三角形,与平面三角形一样由3条边和3个顶点组成,但双曲三角形的内角和小于180度。正如欧几里德几何,任意维度的双曲空间中的三个点也总是共面,因此,双曲平面三角形也描述了在任何更高维度的双曲空间中可能存在的三角形。
根据三角不等式,三角形的其中两边的和必定大于第三边[1][2],此不等式对于边长有限的双曲三角形仍成立[3]。平面三角形若两边的和等于第三边将会退化成内角为0度的退化三角形[4],然而双曲三角形允许内角为0的不退化三角形,这种三角形又称为理想三角形[5]。
定义
双曲三角形和一般的三角形一样,由3个边和3个顶点组成。构成双曲三角形的3个点不落在相同的双曲直线上。同时,这3条边为连接这三个点的双曲线段。[6]
性质
双曲三角形有部分性质与欧几里得几何中的平面三角形类似,例如每个双曲三角形皆存在内切圆,但并非每个双曲三角形都有外接圆。双曲三角形的顶点可以落在双曲极限圆或超圆形上。[7]
具有理想点的三角形
双曲三角形的定义上允许点位于无穷远点,即位于理想边界上的理想点,并保持边位于同一个双曲平面上。如果三角形有一对极限平行(即两个边在往理想点逼近时,距离趋近于零,但不相交),则其将交于无穷远处的理想点,则该点称为欧米加点。该边的夹角为0。这种三角形称为欧米加三角形。[8]
具有理想点的三角形有几个特例:
平行三角形
平行三角形是指有一对边平行的三角形。这个三角形其中一个角对应的顶点为落在无穷远的理想点、另一个角是直角、第三个角是直角和第三个角之间的边平行角。[9]
施魏卡特三角形
两个顶点为理想点且第三个角为直角的三角形。这个三角形是费迪南德·卡尔·施魏卡特首次描述双曲三角形所提及的三角形之一。[10]
理想三角形
所有顶点都是理想点的三角形。所有理想三角形内角和皆为零、面积皆为π。[11]由于双曲三角形的面积取决于内角和(见下节的面积公式),理想三角形是双曲平面中,面积最大的三角形。
标准化高斯曲率
双曲三角形边与角的关系与球面三角形类似,例如:球面几何和双曲几何中,长度尺度都可以利用具有固定角度的等边三角形边长来定义。[12]
若将长度以绝对长度(一种特殊的长度单位,类似于球面几何中的距离之间的关系)来定义,能使不少双曲三角形的公式更为简化。[13]
在庞加莱半平面模型中,绝对长度对应于无穷小的度量 ,在庞加莱圆盘模型中对应于 。
以高斯曲率为负常数 的双曲平面而言,绝对长度的单位长对应到的长度为:
在双曲三角形中,角A、B、C(分别与对应字母的边相对)之和严格小于平角。平角的度数与内角和的差称为该三角形的角亏。双曲三角形的面积等于其角亏(以弧度计)乘以R的平方:
参考文献
- ^ Weisstein, Eric W. (编). Triangle Inequality. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Mohamed A. Khamsi; William A. Kirk. §1.4 The triangle inequality in Rn. An introduction to metric spaces and fixed point theory. Wiley-IEEE. 2001 [2021-08-24]. ISBN 0-471-41825-0. (原始内容存档于2021-10-28).
- ^ A. G. Kovalev (Lecturer). Part IB - Geometry, 4.3 Two models for the hyperbolic plane [IB部 - 几何学,4.3 双曲平面的两种模型]. Dexter Chua. [2021-08-26]. (原始内容存档于2021-08-26) (英语).
- ^ Mathwords: Degenerate. www.mathwords.com. [2019-11-29]. (原始内容存档于2022-03-16).
- ^ Schwartz, Richard Evan. Ideal triangle groups, dented tori, and numerical analysis. Annals of Mathematics. Ser. 2. 2001, 153 (3): 533–598. JSTOR 2661362. MR 1836282. arXiv:math.DG/0105264 . doi:10.2307/2661362.
- ^ Stothers, Wilson, Hyperbolic geometry, University of Glasgow, 2000 [2021-08-24], (原始内容存档于2012-09-06), interactive instructional website
- ^ The circumcircle of a hyperbolic triangle. maths.gla.ac.uk. [2021-08-24]. (原始内容存档于2018-02-11).
- ^ Hyperbolic Geometry Theorem's We Know (PDF). math.uaa.alaska.edu. [2021-08-24]. (原始内容存档 (PDF)于2021-08-29).
- ^ Marvin J. Greenberg (1974) Euclidean and Non-Euclidean Geometries, pp. 211–3, W.H. Freeman & Company.
- ^ Gowers, T. and Barrow-Green, J. and Leader, I. The Princeton Companion to Mathematics. Princeton University Press. 2010. ISBN 9781400830398. LCCN 2008020450.
- ^ Thurston, Dylan. 274 Curves on Surfaces, Lecture 5 (PDF). Fall 2012 [23 July 2013]. (原始内容存档 (PDF)于2022-01-09).
- ^ Sommerville, D.M.Y. The elements of non-Euclidean geometry Unabr. and unaltered republ. Mineola, N.Y.: Dover Publications. 2005: 58. ISBN 0-486-44222-5.
- ^ Needham, Tristan. Visual Complex Analysis. Oxford University Press. 1998: 270 [2021-08-24]. ISBN 9780198534464. (原始内容存档于2021-08-24).
- ^ Ratcliffe, John. Foundations of Hyperbolic Manifolds. Graduate Texts in Mathematics 149. Springer. 2006: 99 [2021-08-24]. ISBN 9780387331973. (原始内容存档于2021-04-29).
That the area of a hyperbolic triangle is proportional to its angle defect first appeared in Lambert's monograph Theorie der Parallellinien, which was published posthumously in 1786.
- ^ Paul Minter (based on Mihalis Dafermos's lectures). Differential Geometry (Part II) [微分几何(第二部)] (PDF). 2016 [2021-08-26]. (原始内容存档 (PDF)于2021-08-29) (英语).
延伸阅读
- Svetlana Katok (1992) Fuchsian Groups, University of Chicago Press ISBN 0-226-42583-5