在微分几何中,高斯-博内定理(亦称高斯-博内公式)是关于曲面的图形(由曲率表征)和拓扑(由欧拉示性数表征)间联系的一项重要表述。它是以卡尔·弗里德里希·高斯和皮埃尔·奥西安·博内命名的,前者发现了定理的一个版本但从未发表,后者1848年发表了该定理的一个特例。
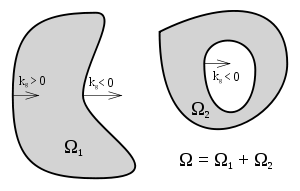
适用高斯-博内定理的复杂区域的一个例子。标示了测地曲率。
定理内容
设 是一个紧的二维黎曼流形, 是其边界。令 为 的高斯曲率, 为 的测地曲率。则有
-
其中dA是该曲面的面积元,ds是M边界的线元。此处 是 的欧拉示性数。
如果 的边界是分段光滑的,我们将 视作光滑部分相应的积分之和,加上光滑部分在曲线边界上的转过的角度之和。
参看
外部链接