黎曼曲面
| 此条目已列出参考文献,但因为没有文内引注而使来源仍然不明。 (2019年5月6日) |
数学上,特别是在复分析中,一个黎曼曲面是一个一维复流形。黎曼曲面可以被视为是一个复平面的变形版本:在每一点局部看来,他们就像一片复平面,但整体的拓扑可能极为不同。例如,他们可以看起来像球或是环,或者两个页面粘在一起。
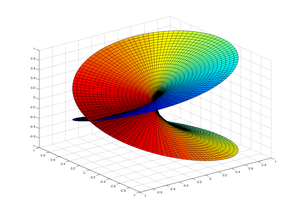
黎曼曲面的精髓在于在曲面之间可以定义全纯函数。黎曼曲面现在被认为是研究这些函数的整体行为的自然选择,特别是像平方根和自然对数这样的多值函数。
每个黎曼曲面都是二维实解析流形(也就是曲面),但它有更多的结构(特别是一个复结构),因为全纯函数的无歧义的定义需要用到这些结构。一个实二维流形可以变成为一个黎曼曲面(通常有几种不同的方式)当且仅当它是可定向的。所以球和环有复结构,但是莫比乌斯带,克莱因瓶和射影平面没有。
黎曼曲面的几何性质是最妙的,它们也给与其它曲线,流形或簇上的推广提供了直观的理解和动力。黎曼-罗赫定理就是这种影响的最佳例子。
形式化定义
令X为一个豪斯多夫空间。一个从开子集U⊂C到X的子集的同胚称为坐标卡。两个有重叠区域的坐标卡f和g称为相容的,如果映射f o g-1和g o f-1是在定义域上全纯的。若A一组相容的图,并且每个X中的x都在某个f的定义域中,则称A为一个图册'。当我们赋予X一个图册A,我们称(X,A)为一个黎曼曲面。如果知道有图册,我们简称X为黎曼曲面。
不同的图册可以在X上给出本质上相同的黎曼曲面结构;为避免这种模糊性,我们有时候要求X为极大的,也就是它不是任何一个更大的图集的子集。根据佐恩引理每个图集A包含于一个唯一的最大图集中。
例子
- 复平面C可能是最平凡的黎曼曲面了。映射f(z) = z(恒等映射)定义了C的一个图,而{f}是C的一个图集。映射g(z) = z*(共轭)映射也定义了C的一个图而{g}也是C的一个图集。图f和g不相容,所以他们各自给了C一个黎曼曲面结构。事实上,给定黎曼曲面X及其图集A,共轭图集B = {f* : f ∈ A}总是不和A相容,因此赋予X一个不同的黎曼曲面结构。
- 类似的,每个复平面的开子集可以自然的视为黎曼曲面。更一般的,每个黎曼曲面的开子集是一个黎曼曲面。
- 令S = C ∪ {∞}并令f(z) = z其中z属于S \ {∞}并且令g(z) = 1 / z其中z属于S \ {0}以及定义1/∞为0.则f和g为图,它们相容,而{ f, g }是S图集,使S成为黎曼曲面。这个特殊的曲面称为黎曼球因为它可以解释为把复平面裹在一个球上。不像复平面,它是一个紧空间。
- 紧黎曼曲面可以视为和定义在复数上的非奇异代数曲线等效。非紧黎曼曲面的重要例子由解析连续给出(见下面)
属性和更多的定义
两个黎曼曲面M和N之间的函数f : M → N称为全纯,如果对于M的图集中的每个图g和N的图集中的每个图h,映射h o f o g-1在所有有定义的地方是全纯的(作为从C到C的函数)。两个全纯函数的复合是全纯的。两个黎曼曲面M和N称为保角等价(或共形等价),如果存在一个双射的从M到N的全纯函数并且其逆也是全纯的(最后一个条件是自动满足的所以可以略去)。两个保角等价的黎曼曲面对于所有的实际应用来讲是完全相同的。
每个单连通的黎曼曲面和C或黎曼球C ∪ {∞}或开圆盘{z ∈ C : |z| < 1}保角等价。这个命题称为单值化定理。
每个连通黎曼曲面可以转成有常数曲率-1,0或1的完备实黎曼流形。这个黎曼结构除了度量的缩放外是唯一。有曲率-1的黎曼曲面称为双曲的;开圆盘是个经典的例子。有曲率0的黎曼曲面称为抛物的;C是典型的抛物黎曼曲面。最后,有曲率+1的黎曼曲面称为椭圆的;黎曼球C ∪ {∞}是这样的一个例子。
对于每个闭抛物黎曼曲面,基本群同构于2阶格群,因而曲面可以构造为C/Γ,其中C是复平面而Γ是格群。陪集的代表的集合叫做基本域。
类似的,对每个双曲黎曼曲面,基本群同构于富克斯群,因而曲面可以由富克斯模型H/Γ构造,其中H是上半平面而Γ是富克斯群。H/Γ陪集的代表是自由正则集,可以作为度量基本多边形。
当一个双曲曲面是紧的,则曲面的总面积是 ,其中g是曲面的亏格;面积可由把高斯-博内定理应用到基本多边形的面积上来算出。
前面我们提到黎曼曲面,象所有复流形,象实流形一样可定向。因为复图f和g有变换函数h = f(g-1(z)),我们可以认为h是从R2开集到R2的映射,在点z的雅可比矩阵也就是由乘以复数h'(z)的运算给出的实线性变换。但是,乘以复数α的行列式等于|α|^2,所以h的雅可比阵有正的行列式值。所以,复图集是可定向图集。
历史
黎曼最早开始研究黎曼曲面。黎曼曲面以他命名。
相关主题
参考
- Hershel M. Farkas and Irwin Kra, Riemann Surfaces (1980), Springer-Verlag, New York. 互联网档案馆) on Planet Math
![f(z) =\sqrt[]{z}](/media/math_img/2172/70e94c0dceaf589d2390621d5697a9dbcbb73c2d.svg)