二十四胞体
| 部分的二十四胞体 | |
|---|---|
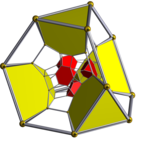 过截角十六胞体(四维) |
 正二十四胞体(四维) |
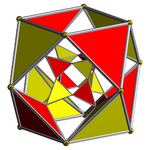 截半超立方体(四维) |
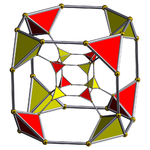 截角超立方体(四维) |
在几何学中,二十四胞体是指有24个胞或维面的多胞体[1]。所有四维或四维以上空间中的二十四胞体共有3个正图形,也就是说有3种正二十四胞体,分别位于四维空间、十二维空间和23维空间,其中四维空间的正二十四胞体称为四维正二十四胞体,由24个正八面体所组成,另两个分别是十二维空间的立方形和23维空间的单纯形。
四维二十四胞体
在四维空间中,二十四胞体为由24个多面体所组成的多胞体,四维空间中唯一具有24个胞的正图形是由24个正八面体所组成的二十四胞体称为正二十四胞体。此外亦存在许多半正的二十四胞体,例如截角超立方体、截角十六胞体等[2]。
| 名称 | 考克斯特 施莱夫利 |
胞 | 图像 | 展开图 |
|---|---|---|---|---|
| 正二十四胞体[3] | {3,4,3}[4] r{3,3,4} = {31,1,1} = |
24个正八面体 | [5] | |
| 截角超立方体 | t{4,3,3} |
8个截角立方体 16个正四面体 |
||
| 截半超立方体[6][7] | = r{4,3,3} = 2r{3,31,1} h3{4,3,3} |
8个截半立方体 16个正四面体 |
||
| 过截角超立方体 过截角十六胞体 |
= 2t{4,3,3} 2t{3,31,1} h2,3{4,3,3} |
8个截角八面体 16个截角四面体 |
||
| 截角十六胞体 | = t{4,3,3} t{3,31,1} h2{4,3,3} |
8个正八面体 16个截角四面体 |
五维二十四胞体
在五维空间中,二十四胞体为由24个四维多胞体所组成的几何形状,但当中不包括任何正图形、办正图形或均匀多胞体。
二十三维正二十四胞体
在二十三维空间几何学中,正二十四胞体是23维空间的一种自身对偶的正多胞体,由24个22维单纯形组成,是一个23维空间中的单纯形。
二十三维正二十四胞体位于其皮特里多边形的正交投影是一个24个顶点的完全图。二十三维正二十四胞体的皮特里多边形是一个扭歪二十四边形,其具有A23的考克斯特群的对称性[8]。
参见
参考文献
- ^ Johnson (2015), Chapter 11, section 11.5 Spherical Coxeter groups, 11.5.5 full polychoric groups
- ^ Klitzing, Richard. 4D uniform polytopes (polychora). bendwavy.org., (x3x3o4o - thex)
- ^ Matila Ghyka, The Geometry of Art and Life (1977), p.68
- ^ Weisstein, Eric W. (编). 24-Cell. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Buekenhout, F. and Parker, M. "The Number of Nets of the Regular Convex Polytopes in Dimension <=4." Disc. Math. 186, 69-94, 1998.
- ^ 2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Model 11, George Olshevsky.
- ^ Klitzing, Richard. 4D uniform polytopes (polychora) o4x3o3o - rit. bendwavy.org.
- ^ Davis, Michael W., The Geometry and Topology of Coxeter Groups (PDF), 2007 [2017-02-24], ISBN 978-0-691-13138-2, Zbl 1142.20020, (原始内容 (PDF)存档于2011-10-09)