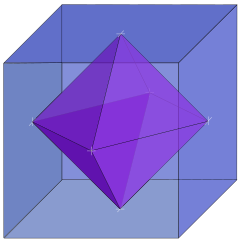
对偶多面体

多面体的对偶多面体有多种种类。最常见的是极点与极线的互换性和拓朴或抽象的对偶性。一种最简单的定义就是若一种多面体的每个顶点均能对应到另一种多面体上的每个面的中心，它就是对方的对偶多面体。

极点与极线互换

在欧几里得空间中，多面体${\displaystyle P}$ 的对偶多面体可以基于一个已知的球之极点与极线互换来定义。在这个定义下，多面体的每个顶点（极点）都与一个平面（极平面）相关联，每个顶点都在一个平面之上，使得由中心向顶点的射线都和平面垂直，且中心和每点的距离的平方等于半径的平方^[5][6]。

若球体的半径为${\displaystyle r}$ 且几何中心位于原点（此时球的方程式可以写为${\displaystyle x^{2}+y^{2}+z^{2}=r^{2}}$ ），则多面体${\displaystyle P}$ 的极点对偶可以定义为：

其中，${\displaystyle q\cdot p}$ 表示${\displaystyle q}$ 和${\displaystyle p}$ 的内积。

若多面体${\displaystyle P}$ 的面之方程式为：

${\displaystyle x_{0}x+y_{0}y+z_{0}z=r^{2}}$ 

则对应对偶多面体${\displaystyle P^{\circ }}$ 的顶点坐标为${\displaystyle (x_{0},y_{0},z_{0})}$ 。类似地，所有${\displaystyle P}$ 的顶点也可以用同样的方式表达为${\displaystyle P^{\circ }}$ 的面。

相应的对偶多面体的顶点就是原来多面体的面的对应，而对偶多面体的面就是原来多面体的顶点的对应。另外，相邻顶点定义出的棱能对应出两个相邻面，这些面的相交线亦定义出对偶多面体的一条棱。

对于具有对称中心的多面体，取对偶所用的球体通常使用以该点为球心的球体，如多尔曼卢克构造（下文提到）。如果多面体无对称中心，但有外接球、内切球或中交球，那么这个多面体也有以使用这个方法来取对偶。而取对偶时也可以使用任意球体，由此产生的对偶多面体形式将取决于球体的大小和位置，随着球体的变化，对偶多面体形式也会随之变化。

这个对偶的概念和射影几何中的对偶相关。

这些规则能一般化到${\displaystyle n}$ 维空间，以定义出对偶多胞形。多胞形的顶点能对应到对偶者的${\displaystyle n-1}$ 维的元素，而${\displaystyle j}$ 点能定义${\displaystyle j-1}$ 维元素，该元素能对应到${\displaystyle j}$ 超平面，${\displaystyle j}$ 超平面相交的位置能给出一个${\displaystyle n-j}$ 维元素。堆砌的对偶也能以近似方式定义。

在拓扑学上，自身对偶多面体是指对偶多面体在拓扑上与原始多面体相等的多面体，并具相同的面、边和顶点的连接方式。理论上，自身对偶多面体和其对偶多面体会有相同的哈斯图。

几何学上的对偶多面体不止要满足拓扑对偶多面体的定义，其要正好是关于某一个点的极倒数，通常是关于其几何中心。几何的自身对偶多面体会与其对偶多面体相似。例如正四面体是一个自身对偶多面体，其对偶多面体是另外一个正四面体，点对称于其几何中心。