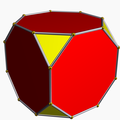
三角化八面体
在几何学中,三角化八面体又称三角三八面体[1][2] 是一种卡塔兰立体,其对偶多面体为截角立方体[3][4],可以视为在正八面体每个面上加入三角锥的结果[5] ,但由于有另一种多面体也是由正八面体每个面上加入三角锥的结果,为大三角化八面体,差别在于大三角化八面体是向内加入角锥[6],而此多面体向外加入角锥,为了区别两者差异,因此有时也会称此多面体为小三角化八面体[4]。
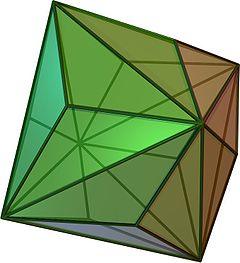 (单击查看旋转模型) | ||||
| 类别 | 卡塔兰立体 | |||
|---|---|---|---|---|
| 对偶多面体 | 截角立方体 | |||
| 识别 | ||||
| 鲍尔斯缩写 | tikko | |||
| 数学表示法 | ||||
| 考克斯特符号 | ||||
| 施莱夫利符号 | dt{4,3} | |||
| 康威表示法 | kO dtC | |||
| 性质 | ||||
| 面 | 24 | |||
| 边 | 36 | |||
| 顶点 | 14 | |||
| 欧拉特征数 | F=24, E=36, V=14 (χ=2) | |||
| 二面角 | 147°21′00″ arccos(−3 + 8√2/17) | |||
| 组成与布局 | ||||
| 面的布局 | V3.8.8 等腰三角形 | |||
| 顶点布局 | 8{3}+6{8} | |||
| 对称性 | ||||
| 对称群 | Oh, B3, [4,3], (*432) | |||
| 旋转对称群 | O, [4,3]+, (432) | |||
| 特性 | ||||
| 凸、面可递 | ||||
| 图像 | ||||
| ||||
在矿物学中,这种形状又称为三八面体[2](英语:trisoctahedron[7][8][4]),部分的矿石可以结晶成这种形状[9],例如萤石[10]。
性质
三角化八面体是一个卡塔兰立体,为阿基米德立体——截角立方体的对偶多面体[4],因此具有面可递的性质。
三角化八面体是一种二十四面体[4],由24个面、36条边和14个顶点组成[11],其中24个面为全等的等腰三角形,顶点可分为2种,一种为8个等腰三角形的公共顶点,另一种为3个等腰三角形的公共顶点。
三角化八面体可以视为将正八面体各个面从中心切割成3个等腰三角形所形成的多面体[12]。
三角化八面体是菱形(正方形倾斜四十五度)四边各加一个等腰三角形拼成的正八边形在立体几何中的推广。
体积与表面积
一个最短边长为1的三角化八面体,它的表面积为 ,体积为 [4]。
面的组成
组成三角化八面体的等腰三角形的2个底角为arccos 约为31.4°[13],由三角形内角关系可知顶角约为117.2°[14][13],边长比为1:1: [15][13]。
顶点坐标
若一个三角化八面体最短边长为2且几何中心位于原点,则其顶点坐标为[16]:
正交投影
三角化八面体有3个特殊的正交投影,分别为于棱上投影、于8个等腰三角形的公共顶点上投影和于3个等腰三角形的公共顶点上投影。
| 投影 对称性 |
[2] | [4] | [6] |
|---|---|---|---|
| 三角化 八面体 |
|||
| 截角 立方体 |
球面镶嵌
三角化八面体也可以表示为球面镶嵌,也可以透过施莱格尔投影,于平面上呈现。而其施莱格尔投影的结果在图论中是一种阿基米德对偶图[17],称为小三角化八面体图[18]。
| 平行投影 | 施莱格尔投影 |
|---|
使用
三角化八面体出现在部分的艺术创作中,例如莫里兹·柯尼利斯·艾雪的艺术创作[19]。部分小说也有使用三角化八面体进行创作,如休伊·库克的系列小说《黑暗时代的编年史》中的《希望之石与奇迹工人》。除了艺术创作外,常见文化也有关于三角化八面体的使用,例如部分的魔术方块和骰子之外型。
相关多面体与镶嵌
三角化八面体可以经由八面体透过三角化变换构造,即将正八面体每个面贴上三角锥来获得。其他也是由正八面体透过康威变换得到的多面体有:
| 对称性: [4,3], (*432) | [4,3]+, (432) | [1+,4,3], (*332) | [4,3+], (3*2) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| {4,3} | t0,1{4,3} | t1{4,3} | t1,2{4,3} | {3,4} | t0,2{4,3} | t0,1,2{4,3} | s{4,3} | h{4,3} | h1,2{4,3} |
| 半正多面体的对偶 | |||||||||
| V4.4.4 | V3.8.8 | V3.4.3.4 | V4.6.6 | V3.3.3.3 | V3.4.4.4 | V4.6.8 | V3.3.3.3.4 | V3.3.3 | V3.3.3.3.3 |
三角化八面体是由等腰三角形组成,且对偶多面体由正八边形与正三角形交错组成。同样由等腰三角形组成,且对偶多面体由正多边形与正三角形交错组成的多面体或镶嵌图包括:
| 对称性 *n32 [n,3] |
球面镶嵌 | 欧氏镶嵌 | 紧凑双曲 | 非紧双曲 | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| 截角镶嵌 | ||||||||
| 顶点 | 3.4.4 | 3.6.6 | 3.8.8 | 3.10.10 | 3.12.12 | 3.14.14 | 3.16.16 | 3.∞.∞ |
| 三角化 镶嵌 |
||||||||
| 顶点 | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ |
类似前面提到的概念,三角化八面体是由等腰三角形组成,且对偶多面体由正八边形与正三角形交错组成。同样由等腰三角形组成,且对偶多面体由正八边形与其他正多边形交错组成的多面体或镶嵌图包括:
| 对称性 *n42 [n,4] |
球面镶嵌 | 欧氏镶嵌 | 紧凑双曲镶嵌 | 仿紧双曲镶嵌 | ||||
|---|---|---|---|---|---|---|---|---|
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | |
| 截角 图 |
||||||||
| 顶点 | 2.8.8 | 3.8.8 | 4.8.8 | 5.8.8 | 6.8.8 | 7.8.8 | 8.8.8 | ∞.8.8 |
| n-角化 图 |
||||||||
| 顶点 | V2.8.8 | V3.8.8 | V4.8.8 | V5.8.8 | V6.8.8 | V7.8.8 | V8.8.8 | V∞.8.8 |
其他三角化八面体
三角化八面体一般是指截角立方体的对偶多面体,但三角化八面体一词原意应为“三角化后的八面体”,换句话说,即在八面体的面上加入三角锥的多面体也可以称为三角化八面体。
| 角锥 高度增加 |
图像 | |||||
|---|---|---|---|---|---|---|
| 种类 | 三角化八面体 | 菱形十二面体 | 星形八面体 | |||
| 加入锥高 (正八面体 边长1) |
+0.099 [4] |
+0.289 |
+0.5 | +0.816 [20] |
+1.5 | |
| 说明 | 加入角锥 至侧面等角 |
加入角锥 至侧面共面 |
加入角锥 使之成为 凹多面体 |
加入正四面体[20] | ||
| 角锥 高度减少 允许负值 (向内加入) |
图像 | |||||
| 种类 | 三角化八面体 | 正八面体 | 凹三角锥八面体 | 大三角化八面体 | ||
| 加入锥高 (正八面体 边长1) |
+0.099 |
0 | -0.408 |
-1 | -1.394 | |
| 说明 | 加入角锥 至侧面等角 |
原始形状 | 向内加入角锥 锥尖抵达几何中心 |
向内加入角锥 锥尖从另一侧凸出 | ||
大三角化八面体
大三角化八面体的是一个拓朴结构与三角化八面体相同的多面体。三角化八面体是由正八面体的每个面上加入角锥构成,而大三角化八面体则是在正八面体的每个面中加入穿过对面的面的倒角锥而成[6],这种在面上加入倒角锥的做法使其与三角化八面体有一样的拓朴结构,几何上的差异在于,大三角化八面体和三角化八面体一个是向外加入角锥[21]、一个是向内加入角锥。
星形八面体
星形八面体一般是指由两个正四面体组合成的复杂多面体,复杂多面体是指该多面体有出现面与面相交的多面体,而简单多面体则是面与面没有自相交情况的多面体。对于与星形八面体外形相同的简单多面体则也可以视为在正八面体每个面阶贴上三角锥的结果,其贴上的三角锥为正四面体[20]。
小三角化八面体图
| 小三角化八面体图 | |
|---|---|
| 度分布 | 3 (8个) 8 (6个) |
| 顶点 | 14 |
| 边 | 36 |
| 半径 | 2 |
| 直径 | 3 |
| 围长 | 3 |
| 色数 | 4 |
| 对偶图 | 截角立方体图 |
| 属性 | 平面, 可积 |
在图论的数学领域中,与三角化八面体相关的图为小三角化八面体图(Small Triakis Octahedral Graph),是三角化八面体之边与顶点的图[18],是一个阿基米德对偶图[17]。
性质
小三角化八面体图有36条边和14个顶点,其中度为3的顶点有8个;度为8的顶点有6个。
参考文献
- Williams, Robert. The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. 1979. ISBN 0-486-23729-X. (Section 3-9)
- Wenninger, Magnus, Dual Models, Cambridge University Press, 1983, ISBN 978-0-521-54325-5, MR 0730208, doi:10.1017/CBO9780511569371 (The thirteen semiregular convex polyhedra and their duals, Page 17, Triakisoctahedron)
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 284, Triakis octahedron)
- ^ Clipart tagged: ‘forms’. etc.usf.edu. [2018-08-28]. (原始内容存档于2018-08-28).
- ^ 2.0 2.1 三八面體 triakisoctahedron (trisoctahedron). 国家教育研究院. [2018-08-27]. (原始内容存档于2018-08-28).
- ^ Catalan Solids: Triakis Octahedron. dmccooey.com. [2018-08-28]. (原始内容存档于2018-02-01).
- ^ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Weisstein, Eric W. (编). Small Triakis Octahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Triakis Octahedron Calculator. rechneronline.de. [2018-08-28]. (原始内容存档于2018-08-28).
- ^ 6.0 6.1 Weisstein, Eric W. (编). 大三角化八面體. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Correns, C. W. Einführung in die Mineralogie (Kristallographie und Petrologie). Berlin: Springer-Verlag. 1949: p. 41.
- ^ Berry, L. G. and Mason, B. Mineralogy: Concepts, Descriptions, Determinations. San Francisco, CA: W. H. Freeman, 1959., p. 127
- ^ 中川宏. 貫入双晶模型の製作 (PDF). [2018-08-30]. (原始内容 (PDF)存档于2018-08-31).
- ^ 高田雅介 著. 日本産鉱物の結晶形態 : 高田鉱物標本・結晶図集. 今井裕之. 2010年4月 (日语).
- ^ triakisoctahedron. bulatov.org. [2018-08-28]. (原始内容存档于2017-12-06).
- ^ geomzome. 三方八面体 The Triakisoctahedron [3,8,8]. 2009-12-26 [2018-08-30]. (原始内容存档于2016-07-25).
- ^ 13.0 13.1 13.2 Triakis octahedron. fillygons.ch. [2018-08-30]. (原始内容存档于2018-08-30).
- ^ Pugh, A. Polyhedra: A Visual Approach. The Dome series. University of California Press: 43. 1976 [2018-08-30]. ISBN 9780520030565. LCCN 74027297. (原始内容存档于2019-06-29).
- ^ Weisstein, E.W. CRC Concise Encyclopedia of Mathematics, Second Edition. CRC Press. 2002: 2732-2733. ISBN 9781420035223.[失效链接]
- ^ Data of Triakis Octahedron. dmccooey.com. [2018-08-30]. (原始内容存档于2017-10-31).
- ^ 17.0 17.1 Weisstein, Eric W. (编). Small Archimedean Dual Graph. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 18.0 18.1 Weisstein, Eric W. (编). Small Triakis Octahedral Graph. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Forty, S. M.C. Escher. Cobham, England: TAJ Books, 2003.
- ^ 20.0 20.1 20.2 Weisstein, Eric W. (编). Stella Octangula. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Weisstein, Eric W. (编). Triakis octahedron. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Klitzing, Richard. 3D convex uniform polyhedra x3o4o - oct. bendwavy.org.
外部链接
- 埃里克·韦斯坦因. Triakis octahedron. MathWorld.、埃里克·韦斯坦因. Catalan solid. MathWorld.
- Triakis Octahedron – Interactive Polyhedron Model
- Virtual Reality Polyhedra(页面存档备份,存于互联网档案馆) www.georgehart.com: The Encyclopedia of Polyhedra
- VRML model(页面存档备份,存于互联网档案馆)
- Conway Notation for Polyhedra(页面存档备份,存于互联网档案馆) Try: "dtC"