2i
是距离原点两个单位的高斯整数[2]:13,为虚数单位的两倍[2]:12,同时也是负四的平方根[2]:12[3][4]:ix[5][6][7][8],是方程式的正虚根[3][9]:10。日常生活中通常不会用来计量事物,例如无法具体地描述何谓个人,逻辑上个人并没有意义。[10]部分书籍或教科书偶尔会使用来做虚数的例子或题目。[11]
| 2i | |
|---|---|
| 数表 — 高斯整数 << −3i −2i −i 0 i 2i 3i >> | |
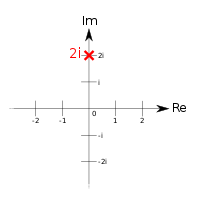 在高斯平面上的位置 | |
| 命名 | |
| 数字 | 2i |
| 名称 | 2i |
| 性质 | |
| 高斯整数分解 | |
| 绝对值 | 2[1] |
| 表示方式 | |
| 值 | |
| 代数形式 | |
| 导航 | ||||||
|---|---|---|---|---|---|---|
| ↑ | ||||||
| 2i | ||||||
| -1+i | i | 1+i | ||||
| ← | -2 | -1 | 0 | 1 | 2 | → |
| -1-i | -i | 1-i | ||||
| -2i | ||||||
| ↓ | ||||||
在高斯平面上,与相邻的纯虚数之高斯整数有和,然而复数不具备有序性,即无法判断与间的大小关系,因此无法定义与何者为的前一个虚数、何者为的下一个虚数。
性质
- 不属于实数,是一个纯虚数,同时也是复数位于复平面,其实部为0、虚部为2[12],辐角为90度( 弧度)[13],其也能表达为 [14]:7或 [15]。
- 是一个高斯整数[16][17][18],高斯整数分解为 [19]:711,或 [20]:433,其中,1+i为2i的高斯素因数。[19]:711[21][22]:247
- 所有复数的可以表达为 之幂的线性组合。[23]换句话说若进位制以 为底数,则可独一无二地表示全体复数[24]。该进制称为2i进制,由高德纳于1955年发现。[25]
- 复数的虚数部可以定义为复数与其共轭复数之差除以 的商,[26]换言之,则 。[2]:32
- 正弦函数可以定义为纯虚指数函数与其倒数之差除以 的商。[27][28]:41[2]:64
- 等于最小的素数和虚数单位的积,即 [15],其中 为第 个素数。
- 虚数单位和虚数单位的倒数相差 。
- 任意数与 相乘的意义为模放大两倍并在复平面上以原点为中心逆时针旋转90度。[14]:7[2]:20-21
2i的幂
的前几次幂为1、 2i、 −4、 −8i、 16、 32i、 −64...[29],其会在实部和虚部交错变换,其单位会在1、i、−1、−i中变化。其中,实数项为−4的幂[30] ,虚数的正值项为16的幂的2倍[31] 、虚数的负值项为16的幂的−8倍[32],因此这种特性使得 作为底数可以不将复数表达为实部与虚部就能表示全体复数,[29]并且有研究以此特性设计复数运算电路[33]。
2i的平方根
的平方根正好是实数单位与虚数单位的和,即 [28]:3,反过来说 正好是实数单位与虚数单位相加的平方, [34][35]:388。
相关数字
−2i
是 的相反数,其平方根曾提议作为复数进位制的底数。[36]
1+i
是 的平方根[28],由于其幂次为1+i、 2i、 −2+2i、 −4、 −4−4i、 −8i...,在正负、虚实交替变化,因此若作为进位制底数可以表达全体复数。但其组合变化相较于 为底数的进位制, 做为底数更为适合。[37]
−1+i
是 的平方根。由于其幂次为−1+i、 −2i、 2+2i、 −4、 4−4i、 8i...,其在正负、虚实交替变化,因此其可以构建一个以 为底数并用1和0表达复数的进位制[36][38]。其他复数虽然也可以,如 ,但对高斯整数而言,以 为底并不是一个优良的选择。[37]
除了 外,其他 形式的复数也能作为进位制底数,但其在表达数的范围不同,以 为例,其表达的范围较为均匀,而 、 等则会越来越狭长。[39]
参见
- 虚数单位
- -2
参考文献
- ^ What is 2i equal to?. geeksforgeeks.org. [2022-09-15]. (原始内容存档于2022-09-15).
- ^ 2.0 2.1 2.2 2.3 2.4 2.5 Mokhithi, Mashudu and Shock, Jonathan, Introduction to Complex Numbers (PDF), Jonathan Shock, 2020 [2022-06-23], (原始内容存档 (PDF)于2022-07-04)
- ^ 3.0 3.1 Complex or Imaginary Numbers. themathpage.com. [2022-06-23]. (原始内容存档于2022-07-13).
- ^ Hart, P. The Book of Imaginary Indians: Ancient Traditions and Modern Caricatures in the White Man's Quest for Meaning. iUniverse. 2008 [2022-06-23]. ISBN 9780595435036. (原始内容存档于2022-08-20).
- ^ A brief history to imaginary numbers. sciencefocus.com. 2019-06-21 [2022-06-23]. (原始内容存档于2022-07-12).
- ^ Williams, Travis D. King Lear, Without the Mathematics: From Reading Mathematics to Reading Mathematically. The Palgrave Handbook of Literature and Mathematics (Springer). 2021: 399–418.
- ^ Neuman, Yrsa. Moore’s Paradox and Limits in Language Use. Wittgenstein and the Limits of Language (Routledge). 2019: 159–171.
- ^ Parker, Barry. Fractals. Chaos in the Cosmos (Springer). 1996: 129–154.
- ^ Complex Numbers and the Complex Exponential (PDF). people.math.wisc.edu. [2022-06-23]. (原始内容存档 (PDF)于2022-01-21).
- ^ Abubakr, Mohammed. On logical extension of algebraic division. arXiv preprint arXiv:1101.2798. 2011 [2022-06-23]. doi:10.48550/ARXIV.1101.2798. (原始内容存档于2022-07-04).
- ^ 中学数学实用词典, 九章出版社, 孙文先, P.22 中的示范其解为2i,
- ^ All Complex Number Solutions z=2i. mathway.com. [2022-06-23]. (原始内容存档于2022-06-25).
- ^ 14.0 14.1 Jeremy Orloff. Complex algebra and the complex plane (PDF). math.mit.edu. [2022-06-23]. (原始内容存档 (PDF)于2021-11-03).
- ^ 15.0 15.1 Wolfram, Stephen. "(smallest prime number) * (imaginary unit)". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research (英语).
- ^ C. F. Gauss, Theoria residuorum biquadraticorum. Commentatio secunda., Comm. Soc. Reg. Sci. Gottingen 7 (1832) 1-34; reprinted in Werke, Georg Olms Verlag, Hildesheim, 1973, pp. 93-148.
- ^ 从数到环:环论的早期历史 (页面存档备份,存于互联网档案馆),由Israel Kleiner所作 (Elem. Math. 53 (1998) 18 – 35)
- ^ Ribenboim, Paulo, The New Book of Prime Number Records, New York: Springer, 1996, ISBN 0-387-94457-5
- ^ 19.0 19.1 Banerjee, Ashmi and Mukherjee, Shaunak and Datta, Somjit and Majumder, Subhashis. Computational search for Gaussian perfect integers. 2015 International Conference on Control Communication & Computing India (ICCC) (IEEE). 2015: 710–715 [2022-08-15]. (原始内容存档于2022-08-15).
- ^ Briggs, WE. Factorization in Integral Domains. The Mathematics Teacher (National Council of Teachers of Mathematics). 1966, 59 (5): 432–436.
- ^ Kerins, Bowen. Delving Deeper: Gauss, Pythagoras, and Heron. The Mathematics Teacher (National Council of Teachers of Mathematics). 2003, 96 (5): 350–357.
- ^ Gallian, Joseph A and Jungreis, Douglas S. Homomorphisms from Zm[i] into Zn[i] and Zm[ρ] into Zn[ρ], Where i2 + 1 = 0 and ρ2 + ρ + 1 = 0. The American Mathematical Monthly (Taylor & Francis). 1988, 95 (3): 247–249.
- ^ Blest, David C and Jamil, Tariq. Division in a binary representation for complex numbers. International Journal of Mathematical Education in Science and Technology (Taylor & Francis). 2003, 34 (4): 561–574.
- ^ Donald Knuth. An imaginary number system. Communications of the ACM. April 1960, 3 (4).
- ^ D. Knuth. The Art of Computer Programming. Volume 2, 3rd Edition. Addison-Wesley. pp. 205, "Positional Number Systems"
- ^ Complex Numbers (PDF), hawaii.edu, [2022-06-23], (原始内容存档 (PDF)于2022-06-26)
- ^ Weisstein, Eric W. (编). Sine. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ 28.0 28.1 28.2 Bak, Joseph and Newman, Donald J and Newman, Donald J, Complex analysis (PDF) 8, Springer, 2010 [2022-06-23], (原始内容存档 (PDF)于2022-06-25)
- ^ 29.0 29.1 Robert Braunwart. Negative and Imaginary Radices. School Science and Mathematics. 1965-04, 65 (4): 292–295 [2022-06-23]. doi:10.1111/j.1949-8594.1965.tb13422.x. (原始内容存档于2022-06-27) (英语).
- ^ Sloane, N.J.A. (编). Sequence A262710 (Powers of -4). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N.J.A. (编). Sequence A013776 (a(n) = a(n) = 2^(4*n+1)). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sloane, N.J.A. (编). Sequence A013777 (a(n) = 2^(4*n + 3)). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Sarkar, Souradip and Gomony, Manil Dev. Quater-imaginary base for complex number arithmetic circuits. 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE) (IEEE). 2018: 1481–1483 [2022-08-15]. (原始内容存档于2022-08-20).
- ^ Dujella, Andrej. The problem of Diophantus and Davenport for Gaussian integer. Glasnik Matematicki (HRVATSKO MATEMATICKO DRUSTVO). 1997, 32: 1–10.
- ^ Collins, George E. A fast Euclidean algorithm for Gaussian integers. Journal of Symbolic Computation (Elsevier). 2002, 33 (4): 385–392.
- ^ 36.0 36.1 Penney, Walter. A``Binary System for Complex Numbers (PDF). J. ACM. 1965, 12 (2): 247–248 [2022-06-23]. (原始内容存档 (PDF)于2022-07-04).
- ^ 37.0 37.1 Gilbert, William J. Fractal geometry derived from complex bases (PDF). The Mathematical Intelligencer (Springer). 1982, 4 (2): 78–86 [2022-06-23]. (原始内容存档 (PDF)于2022-01-02).
- ^ Gilbert, William J. Arithmetic in complex bases. Mathematics Magazine (Taylor & Francis). 1984, 57 (2): 77–81.
- ^ Gilbert, William J. The fractal dimension of sets derived from complex bases (PDF). Canadian mathematical bulletin (Cambridge University Press). 1986, 29 (4): 495–500 [2022-08-20]. (原始内容存档 (PDF)于2022-08-20).






