泛函

泛函（functional）指以函数构成的向量空间为定义域，实数为值域为的“函数”，即某一个依赖于其它一个或者几个函数确定其值的量，往往被称为“函数的函数”。在泛函分析中，泛函也用来指一个从任意向量空间到标量域的映射。泛函中的一类特例线性泛函引发了对对偶空间的研究。泛函的应用可以追溯到变分法，其中通常需要寻找一个函数用来最小化某个特定泛函。在物理学上，寻找某个能量泛函的最小系统状态是泛函的一个重要应用。

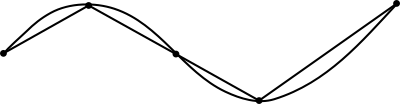
弧长泛函以可求长曲线组成的向量空间（

C([0,1],\mathbb {R} ^{3})

的一个子集）为定义域，以实标量为输出值。这是一个非线性泛函的例子。

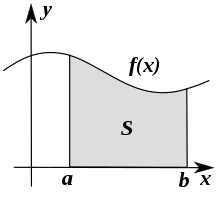
黎曼积分是以从

\mathbb {R}

到

\mathbb {R}

的黎曼可积函数组成的向量空间为定义域的线性泛函。

设 $S\$ 是由一些函数构成的集合。所谓 $S\$ 上的泛函就是 $S\$ 上的一个实值函数。 $S\$ 称为该泛函的容许函数集。

函数的变换某种程度上是更一般的概念，参见算子。

例子

设在 xOy 平面上有一簇曲线 $y(x)$ , 其长度为 $L=\int _{C}ds=\int _{x_{0}}^{x_{1}}{\sqrt {1+{y'}^{2}}}dx$ 。

显然， $y(x)$ 不同, $L$ 也不同，即 $L$ 的数值依赖于整个函数 $y(x)$ 而改变。 $L$ 和函数 $y(x)$ 之间的这种依赖关系就称为泛函关系。

性质

对偶性

观察映射

x_{0}\mapsto f(x_{0})

是一个函数，在这里， $x_{0}$ 是函数f的自变量。

同时，将函数映射至一个点的函数值

f\mapsto f(x_{0})

是一个泛函，在此 $x_{0}$ 是一个参数

只要 $f$ 是一个从向量空间至一个布于实数的体的线性转换，上述的线性映射彼此对偶，那么在泛函分析上，这两者都称作线性泛函。

参见

线性泛函
最优化
张量

参考资料

Rowland, Todd. Functional. MathWorld.
Lang, Serge, III. Modules, §6. The dual space and dual module, Algebra, Graduate Texts in Mathematics 211 Revised third, New York: Springer-Verlag: 142–146, 2002, ISBN 978-0-387-95385-4, MR1878556