十二面体

部分的十二面体
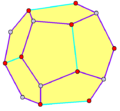五角十二面体	扭棱楔形体
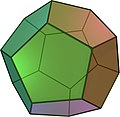正十二面体	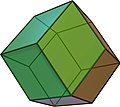菱形十二面体
正十角柱（英语：Decagonal prism）	双四角锥柱

在几何学中，十二面体是指由十二个面组成的多面体，而由十二个全等的正五边形组成的十二面体称为正十二面体。

十二个面的多面体可以是正十二面体、菱形十二面体、正五角帐塔、双四角锥柱、扭棱锲形体、十一角锥、十角柱。

在许多情况下，常用“十二面体”一词来代表正十二面体。

常见的十二面体

在所有凸十二面体中，包含镜射像共有6,384,634种拓朴结构明显差异的凸十二面体^[1]^[2]。拓朴结构有明显差异意味着两种多面体无法透过移动顶点位置、扭曲或伸缩来相互变换的多面体，例如正十二面体和十角柱无论如何变形都无法互相变换，因此拓朴结构不同，但正十二面体和截角五方偏方面体可以透过简单的变形来彼此互换，因此正十二面体和截角五方偏方面体在拓朴上并无明显差异。

十角柱

正十角柱

十角柱是一种底面为十边形的柱体，是十二面体的一种，由12个面、30条边和20个顶点组成。正十角柱代表每个面都是正多边形的十角柱，其每个顶点都是2个正方形和1个十边形的公共顶点，因此具有每个角等角的性质，可以归类为半正十二面体。而顶点都是2个正方形和1个十边形的公共顶点的这种顶角，在顶点图中以 $4{.}4{.}10$ 表示。正十角柱在施莱夫利符号中可以利用{10}×{} 或 t{2, 10}来表示；在考克斯特—迪肯符号（英语：Coxeter-Dynkin diagram）中可以利用来表示；在威佐夫符号（英语：Wythoff symbol）中可以利用2 10 | 2来表示；在康威多面体表示法中可以利用P10来表示。若一个正十角柱底边的边长为 $s$ 、高为 $h$ ，则其体积 $V$ 和表面积 $S$ 为^[3]：

V={\frac {5{\sqrt {5+2{\sqrt {5}}}}}{2}}hs^{2}\approx 7.69421hs^{2}

S=5s\left(2h+{\sqrt {5+2{\sqrt {5}}}}s\right)\approx 5s\left(2h+3.07768s\right)

十一角锥

十一角锥是一种底面为十一边形的锥体，是十二面体的一种，其具有12个面、22条边和12个顶点，其对偶多面体是自己本身^[4]。正十一角锥是一种底面为正十一边形的十一角锥。若一个正十一角锥底边的边长为 $s$ 、高为 $h$ ，则其体积 $V$ 和表面积 $S$ 为^[4]：

V={\frac {11hs^{2}\cot {\frac {\pi }{11}}}{12}}\approx 3.12188hs^{2}

S={\frac {11s\left({\sqrt {4h^{2}+s^{2}\cot ^{2}{\frac {\pi }{11}}}}+s\cot {\frac {\pi }{11}}\right)}{4}}\approx 2.75s\left({\sqrt {4h^{2}+11.5987s^{2}}}+3.40569s\right)

双六角锥

双六角锥是一种以六边形为基底的双锥体，是十二面体的一种，其可以视为两个六角锥底面对底面叠合成的立体，由12个面、18条边和8个顶点组成^[5]，对偶多面体为六角柱^[5]。

侧锥七角柱

侧锥七角柱是指在七角柱的侧面上叠上锥体所构成的立体。侧锥七角柱，是十二面体的一种，共由12个面、25条边和15个顶点所组成。当侧锥七角柱的所有面都是正多边形时，其侧锥的侧面与七角柱侧面的角度将会超过180度（约为183.3度）为接近平角的优角：

{\frac {5\pi }{7}}+\arccos {\left({\frac {1}{\sqrt {3}}}\right)}\approx 3.19931137\approx 183.3070388888^{\circ }

因为有超过180度的内角，因此这种多面体是凹多面体，故不属于詹森多面体。底面边数最高且属于詹森多面体多面体的侧锥柱体只到六角柱，即侧锥六角柱，其中，侧锥六角柱的侧锥与侧面的角度也十分接近平角的180度（约为174.7度）：

\arccos {\left(-{\frac {1}{2}}\right)}+\arccos {\left({\frac {1}{\sqrt {3}}}\right)}\approx 3.04971172\approx 174.73561^{\circ }

侧锥七角柱
侧锥六角柱

六方偏方面体

在几何学中，六方偏方面体（英语：Hexagonal Trapezohedron）是一个由12个全等的筝形组成的多面体，为六角反角柱的对偶。所有六方偏方面体都有12个面、24条边和14个顶点^[6]。

复三方偏三角面体

复三方偏三角面体（ditrigonal scalenohedron）^[7]又称为六方偏三角面体（Hexagonal Scalenohedron），是指具有三角形二面体对称性的偏三角面体，可以视为底为扭歪六边形的双六角锥，由12个全等的不等边三角形组成^[8]^:245，共有12个面、18个边和8个顶点。在矿物学中，复三方偏三角面体是一种晶族^[9]，部分晶体的晶形可以呈复三方偏三角面体形状，例如炉甘石^[10]^:107和方解石。

复三方偏三角面体
晶形呈复三方偏三角面体的方解石

詹森多面体

在十一面体中，有4个是詹森多面体，它们分别为：正五角帐塔、扭棱锲形体、双四角锥柱、正二十面体欠二侧锥（英语：Metabidiminished icosahedron）。

名称	种类	编号	顶点	边	面	面的种类	对称性
正五角帐塔	帐塔	J₅	15	25	12	5个正三角形 5个正方形 1个正五边形 1个正十边形	C_5v, [5], (*55)
扭棱锲形体	变棱锥	J₈₄	8	18	12	12个正三角形	D_2d
双四角锥柱	双锥柱	J₁₅	10	20	12	8个正三角形 4个正方形	D_4h, [4,2], (*422)
正二十面体欠二侧锥	切割二十面体	J₆₂	10	20	12	10个正三角形 2个五边形	C_2v

十二面体列表

名称	种类	符号	顶点	边	面	χ	面的种类	对称性
正十二面体	正多面体	{5,3}	20	30^[11]	12	2	12个正五边形	I_h, H₃, [5,3], (*532)
十角柱	棱柱体	t{2,10} {10}x{}	20	30^[12]	12	2	2个十边形 10个矩形	D_10h, [8,2], (*10 2 2), order 40
十一角锥	棱锥体	( )∨{11}	12	22	12	2	1个十一边形 11个三角形	C_11v, [11], (*11 11)^[13]
双六角锥	双锥体	{ }+{6}	8	18	12	2	12个三角形	D_6h, [6,2], (*226), order 24
五角反柱	反棱柱	s{2,5}	10	20	12	2	2个五边形 10个三角形	D_5d, [2⁺,10], (2*5), order 20
截对角五方偏方面体	截对角偏方面体		20	30	12	2	2个五边形底面 10个五边形侧面	D_5d, [2⁺,10], (2*5), 20阶

常见的十二面体
I_h, 120阶
正-	小星形-	大-	大星形-

T_h, 24阶	T, 12阶	O_h, 48阶	T_d, 24阶
五角十二面体	五角三四面体	菱形-	筝形-

D_4h, 16阶		D_3h, 12阶
菱形六角化-	菱形四角化-	梯形菱形-	梯形筝形-

参见

正十二面体烷（化学）

参考文献

^ Steven Dutch: How Many Polyhedra are There? （页面存档备份，存于互联网档案馆）
^ Counting polyhedra （页面存档备份，存于互联网档案馆） numericana.com [2016-1-10]
^ Wolfram, Stephen. "decagon prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
^ ^4.0 ^4.1 Wolfram, Stephen. "Hendecagon pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.
^ ^5.0 ^5.1 David I. McCooey. Simplest Canonical Polyhedron with D6h Symmetry: Hexagonal Dipyramid).
^ Dipyramids & Trapezohedra: Hexagonal Trapezohedron. dmccooey.com.
^ 複三方偏三角面體 ditrigonal scalenohedron. 乐词网, 国家教育研究院.
^ 台湾商务印书馆. 编审委员会. 增修辭源, 第 1 卷. 增修辞源. 台湾商务印书馆. 1979 [2023-01-08]. ISBN 9789570513738. （原始内容存档于2023-01-08）.
^ 複三方偏三角面晶族 ditrigonal scalenohedral class. 乐词网, 国家教育研究院.
^ 中國壯藥材：壯漢文化交流的結晶. 崧烨文化. 2019. ISBN 9789576819933.
^ Sutton, Daud, Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA: 55, 2002 [2016-08-14], ISBN 9780802713865, （原始内容存档于2016-08-01）
^ The Decagonal Prism. eusebeia. [2016-08-21]. （原始内容存档于2016-04-13）.
^ Simplest Canonical Polyhedron with C11v Symmetry. dmccooey. [2016-08-21]. （原始内容存档于2016-08-07）.

[1] Steven Dutch: How Many Polyhedra are There? （页面存档备份，存于互联网档案馆）

[2] Counting polyhedra （页面存档备份，存于互联网档案馆） numericana.com [2016-1-10]

[decagon_prism-3] Wolfram, Stephen. "decagon prism". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.

[Hendecagon_pyramid-4] 4.0 ^4.1 Wolfram, Stephen. "Hendecagon pyramid". from Wolfram Alpha: Computational Knowledge Engine, Wolfram Research （英语）.

[Simplest_Canonical_Polyhedron_with_D6h_Symmetry_dmccooey-5] 5.0 ^5.1 David I. McCooey. Simplest Canonical Polyhedron with D6h Symmetry: Hexagonal Dipyramid).

[6] Dipyramids & Trapezohedra: Hexagonal Trapezohedron. dmccooey.com.

[7] 複三方偏三角面體 ditrigonal scalenohedron. 乐词网, 国家教育研究院.

[book_臺灣商務印書館1979增修辭源-8] 台湾商务印书馆. 编审委员会. 增修辭源, 第 1 卷. 增修辞源. 台湾商务印书馆. 1979 [2023-01-08]. ISBN 9789570513738. （原始内容存档于2023-01-08）.

[9] 複三方偏三角面晶族 ditrigonal scalenohedral class. 乐词网, 国家教育研究院.

[book_2019中國壯藥材-10] 中國壯藥材：壯漢文化交流的結晶. 崧烨文化. 2019. ISBN 9789576819933.

[11] Sutton, Daud, Platonic & Archimedean Solids, Wooden Books, Bloomsbury Publishing USA: 55, 2002 [2016-08-14], ISBN 9780802713865, （原始内容存档于2016-08-01）

[12] The Decagonal Prism. eusebeia. [2016-08-21]. （原始内容存档于2016-04-13）.

[13] Simplest Canonical Polyhedron with C11v Symmetry. dmccooey. [2016-08-21]. （原始内容存档于2016-08-07）.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]