四维正十一胞体
在四维空间几何学中,正十一胞体是四维空间的一种自身对偶[1]的抽象正多胞形[2],由11个二十面体半形组成[3]。
| 正十一胞体 | |
|---|---|
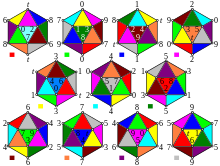 | |
| 类型 | 抽象正多胞形 |
| 家族 | 抽象多胞形 |
| 维度 | 4 |
| 对偶多胞形 | 正十一胞体(自身对偶) |
| 数学表示法 | |
| 施莱夫利符号 | {3,5,3} |
| 性质 | |
| 胞 | 11个二十面体半形 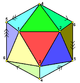 |
| 面 | 55个三角形 |
| 边 | 55 |
| 顶点 | 11 |
| 组成与布局 | |
| 顶点图 |  十二面体半形 |
| 对称性 | |
| 对称群 | L2(11) (order 660) |
| 特性 | |
| 抽象、正 | |
性质
四维正十一胞体共有11个胞、55个面、55条边和11个顶点,其对偶多胞体为自己本身,是一个自身对偶的多胞体。其具有射影线性群 L2(11) 的对称性,因此其对称性阶数为660。
四维正十一胞体的每个顶点都是三个二十面体半形的公共顶点,因此在施莱夫利符号中,四维正十一胞体可以用{3,5,3}表示,但是此种表示法有歧义,会与正二十面体堆砌冲突,其胞二十面体半形在施莱夫利符号中亦与正二十面体{3,5}冲突,因此有时会将四维正十一胞体的施莱夫利符号以 {{3,5}5,{5,3}5} 表示[4]。
历史
1977年时,布兰科·格林鲍姆尝试将二十面体半形边与边组合起来,直到形成封闭区域,因而发现了四维正十一胞体。1984年时,考克斯特在更深入研究对称性时也发现了四维正十一胞体,两人都是独立发现四维正十一饱体。 著名物理学家弗里曼·戴森也对这种形状十分感兴趣,并在一篇文章说道:“帕雷托知道这件事应该会很高兴。”[5]
相关多胞体
十维正十一胞体的正投影图,包含11个顶点和55条边。
这个四维的抽象十一胞体的边数与十维正十一胞体的边数一样多,且含其面数165的三分之一。因此,在十维空间中可以被描绘为正图形,不过它的胞是扭歪多面体,换句话说,每个胞的每一个顶点并不位于同一个欧式三维子空间中。
参见
参考文献
- ^ B. Grünbaum, Regularity of Graphs, Complexes and Designs. Colloque Internationaux C.N.R.S., No 290, Problèmes Combinatoires et Théorie des Graphes, (Orsay 1976), pp 191-197.
- ^ Peter McMullen, Egon Schulte, Abstract Regular Polytopes, Cambridge University Press, 2002. Coxeter, H.S.M., A Symmetrical Arrangement of Eleven hemi-Icosahedra, Annals of Discrete Mathematics 20 pp103–114.
- ^ Polytope of Type {3,5,3}. abstract-polytopes.com. [2016-08-19].
- ^ [1] (页面存档备份,存于互联网档案馆) 2007 ISAMA paper: Hyperseeing the Regular Hendecachoron, Carlo H. Séquin & Jaron Lanier, Also Isama 2007, Texas A&m hyper-Seeing the Regular Hendeca-choron. (= 11-Cell) Archive.is的存档,存档日期2013-08-28
外部链接
- J. Lanier, Jaron’s World. Discover, April 2007, pp 28-29.(页面存档备份,存于互联网档案馆)
- Klitzing, Richard. Explanations Grünbaum-Coxeter Polytopes. bendwavy.org.