五阶正方形镶嵌
在几何学中,五阶正方形镶嵌是由正方形组成的双曲正镶嵌图,在施莱夫利符号中用{4,5}表示,代表了每个顶点皆为五个正方形的公共顶点,因此每个顶点周围皆包含了五个不重叠的正方形,一个正方形内角90度,五个正方形超过了360度,因此无法因此无法在平面上作出,但可以在双曲面上作出,或是以扭歪多面体的方式呈现。
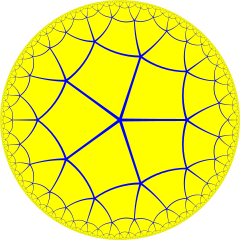 庞加莱圆盘模型 | ||
| 类别 | 双曲正镶嵌 | |
|---|---|---|
| 对偶多面体 | 四阶五边形镶嵌 | |
| 识别 | ||
| 鲍尔斯缩写 | pesquat | |
| 数学表示法 | ||
| 考克斯特符号 | ||
| 施莱夫利符号 | {4,5} | |
| 威佐夫符号 | 5 | 4 2 | |
| 组成与布局 | ||
| 顶点图 | 45 | |
| 对称性 | ||
| 对称群 | [5,4], (*542) | |
| 旋转对称群 | [5,4]+, (542) | |
| 特性 | ||
| 正、非严格凸、紧凑 | ||
| 图像 | ||
| ||
性质
五阶正方形镶嵌由正方形组成,且每个顶点都是5个正方形的公共顶点,在施莱夫利符号中用{4,5}表示[1]。由于平面上镶嵌了四个正方形就满了,因此若要镶嵌五个正方形来使每个顶点都是5个正方形的公共顶点的话,仅能将镶嵌的面扭曲成双曲面
| 一个五阶正方形镶嵌的纸模型,可以看到它不是一个平面,像是一个马鞍面 |
相关多面体及镶嵌
| 球面镶嵌 | 双曲面镶嵌 | |||||||
|---|---|---|---|---|---|---|---|---|
| {2,5} |
{3,5} |
{4,5} |
{5,5} |
{6,5} |
{7,5} |
{8,5} |
... | {∞,5} |
五阶正方形镶嵌在拓扑上与一系列用施莱夫利符号{4,n}表示且顶点图为4n的(广义)多面体一直延伸到双曲镶嵌:
| 有限 | 欧氏 | 双曲紧空间 | 仿紧空间 | 非紧 | |||
|---|---|---|---|---|---|---|---|
| {4,3} |
{4,4} |
{4,5} |
{4,6} |
{4,7} |
{4,8}... |
{4,∞} |
{4,iπ/λ} |
五阶正方形镶嵌可以透过截角操作或其他康威变换得到一系列与之相关的半正镶嵌,其与五阶正方形镶嵌拥有相似的对称性[5,4], (*542)或[5,4]+(542):
| 对称性: [5,4], (*542) | [5,4]+, (542) | [5+,4], (5*2) | [5,4,1+], (*552) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| {5,4} | t{5,4} | r{5,4} | 2t{5,4}=t{4,5} | 2r{5,4}={4,5} | rr{5,4} | tr{5,4} | sr{5,4} | s{5,4} | h{4,5} | |
| 半正对偶 | ||||||||||
| V54 | V4.10.10 | V4.5.4.5 | V5.8.8 | V45 | V4.4.5.4 | V4.8.10 | V3.3.4.3.5 | V3.3.5.3.5 | V55 | |
五阶正方形镶嵌的双曲镶嵌可以反过来多面体化构造进欧几里得空间而得到半正扭歪无限面体[2]。
构成的蜂巢体
有一些蜂巢体由五阶正方形镶嵌为胞构成
参见
参考文献
- ^ The dual tessellation {4,5} of the hyperbolic plane. clarku.edu.
- ^ {4,5}. superliminal.com.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 0-486-40919-8. LCCN 99035678.
外部链接
- 埃里克·韦斯坦因. Hyperbolic tiling. MathWorld.
- 埃里克·韦斯坦因. Poincaré hyperbolic disk. MathWorld.
- Hyperbolic and Spherical Tiling Gallery(页面存档备份,存于互联网档案馆)
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings (页面存档备份,存于互联网档案馆)
- Hyperbolic Planar Tessellations, Don Hatch(页面存档备份,存于互联网档案馆)
