提示
提示:此条目的主题不是
驻点、
滞点或
临界点。
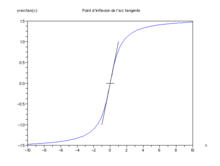
拐点(英语:Inflection point)或称反曲点,是一条连续曲线由凸转凹,或由凹转凸的点,或者等价地说,是使切线穿越曲线的点。
决定曲线的拐点有助于理解曲线的外形,这在描绘曲线图形时特别有用。
定义
若曲线图形在一点由凸转凹,或由凹转凸,则称此点为拐点。直观地说,拐点是使切线穿越曲线的点。
若该曲线图形的函数在某点的二阶导数为零或不存在,且二阶导数在该点两侧符号相反,该点即为函数的拐点。这是寻找拐点时最实用的方法之一。
拐点的必要条件
拐点的必要条件:设 在 内二阶可导, ,若 是曲线 的一个拐点,则 。
比如, ,有 ,但是0两侧全是凸,所以0不是函数 的拐点。
拐点的充分条件:设 在 内二阶可导, ,若在 两侧附近 异号,则点 为曲线的拐点。否则(即 保持同号), 不是拐点。
分类
拐点可以根据 为零或不为零,进行分类:
- 如果 为零,此点为拐点的驻点,简称为鞍点。
- 如果 不为零,此点为拐点的非驻点。
例如: 的点 是一个鞍点,切线为 轴,切线正好将图像分为两半。
参数曲线的拐点
平面参数曲线的拐点是使其曲率变号的点,此时曲率中心(居于曲线凹侧)从曲线的一侧换至另一侧。
双正则点与拐点
双正则点是使得参数曲线的一阶与二阶微分(它们是向量)线性无关的点。在双正则点上,曲线既无拐点亦非直线。在非双正则点上曲率为零,但是不一定有变号。在寻找参数曲线的拐点时,我们通常先以微分找出非双正则点,继之研究其局部性状,以判定是否为拐点。
注:某些作者偏好将拐点定义为“使一阶与二阶微分平行的点”,在此定义下,切线不一定在该点穿越曲线本身。
代数曲线的拐点
设 为域 上的平面代数曲线,其拐点定义为一平滑点 ,使得该点切线 与 在 点的相交重数 。
注意到一条曲线与 在 点相切的充要条件是相交重数 。当 时,代数曲线的拐点定义等价于上节注记中的广义定义。
参见
文献
- Robin Hartshorne (1997). Algebraic Geometry. Springer-Verlag. ISBN 0-387-90244-9.