在概率论和统计学中,指数分布(英语:Exponential distribution)是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进入机场的时间间隔、电话打进客服中心的时间间隔、中文维基百科新条目出现的时间间隔、机器的寿命等。
指数分配|
概率密度函数 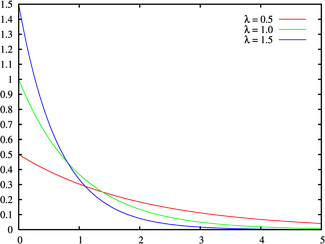 |
|
累积分布函数 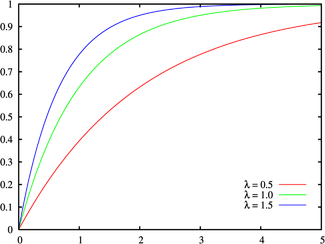 |
| 参数 |
 率 率 |
|---|
| 值域 |
 |
|---|
| 概率密度函数 |
 |
|---|
| 累积分布函数 |
 |
|---|
| 期望值 |
 |
|---|
| 中位数 |
 |
|---|
| 众数 |
 |
|---|
| 方差 |
 |
|---|
| 偏度 |
 |
|---|
| 峰度 |
 |
|---|
| 熵 |
 |
|---|
| 矩生成函数 |
 |
|---|
| 特征函数 |
 |
|---|
记号
指数分布即形状参数α为1的伽玛分布。
若随机变量 服从参数为 或 的指数分布,则记作
或
两者意义相同,只是 与 互为倒数关系。只要将以下式子做 的替换即可,即,指数分布之概率密度函数为:
-
或
-
累积分布函数为:
-
或
-
其中λ > 0是分布的参数,即每单位时间发生该事件的次数; β 为尺度参数,即该事件在每单位时间内的发生率。两者常被称为率参数(rate parameter)。指数分布的区间是[0,∞)。
特性
期望值与方差
随机变量X (X 的参数为λ或β) 的期望值是:
-
例如:如果你平均每个小时接到2次电话,那么你预期等待每一次电话的时间是半个小时。
X 的方差是:
-
X 的偏态系数是:
V[X] = 1
无记忆性
指数函数的一个重要特征是无记忆性(Memoryless Property,又称遗失记忆性)。这表示如果一个随机变量呈指数分布,它的条件概率遵循:
-
与泊松过程的关系
泊松过程是一种重要的随机过程。泊松过程中,第k次随机事件与第k+1次随机事件出现的时间间隔服从指数分布。而根据泊松过程的定义,长度为t的时间段内没有随机事件出现的概率等于
- ,
长度为t的时间段内随机事件发生一次的概率等于
,
所以第k次随机事件之后长度为t的时间段内,第k+n次 (n=1, 2, 3,...)随机事件出现的概率等于 。这是指数分布。这还表明了泊松过程的无记忆性。
四分位数
率参数λ的四分位数函数(Quartile function)是:
-
- 第一四分位数:
- 中位数:
- 第三四分位数:
因此,四分位距为ln(3)/λ。
参数估计
最大似然法
给定独立同分布样本x = (x1, ..., xn),λ的似然函数(Likelihood function)是:
-
其中:
- 是样本期望値。
似然函数对数的导数是:
-
参数λ的最大似然估计(Maximum likelihood)值是:
-
参见
参考文献
- Donald E. Knuth (1998). The Art of Computer Programming, volume 2: Seminumerical Algorithms, 3rd edn. Boston: Addison-Wesley. 编辑














