此条目需要精通或熟悉相关主题的编者参与及协助编辑。 (2012年9月2日)
请邀请适合的人士改善本条目。更多的细节与详情请参见讨论页。 |
在概率论中,马尔可夫不等式(英语:Markov's inequality)给出了随机变量的函数大于等于某正数的概率的上界。虽然它以俄国数学家安德雷·马尔可夫命名,但该不等式曾出现在一些更早的文献中,其中包括马尔可夫的老师--巴夫尼提·列波维奇·切比雪夫。
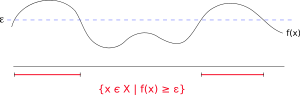
马尔可夫不等式提供了

超过某特定数值

(图中标示红色线处)概率的上界,其上界包括了特定数值

及

的平均值
马尔可夫不等式把概率关联到数学期望,给出了随机变量的累积分布函数一个宽泛但仍有用的界。
马尔可夫不等式的一个应用是,不超过1/5的人口会有超过5倍于人均收入的收入。
表达式
X为一非负随机变量,则
- [1]
若用测度领域的术语来表示,马尔可夫不等式可表示为若(X, Σ, μ)是一个测度空间,ƒ为可测的扩展实数的函数,且 ,则
-
有时上述的不等式会被称为切比雪夫不等式[2]。
对于单调增加函数的扩展版本
若φ是定义在非负实数上的单调增加函数,且其值非负,X是一个随机变量,a ≥ 0,且φ(a) > 0,则
-
证明
-
用来推导切比雪夫不等式
切比雪夫不等式使用方差来作为一随机变量超过平均值概率的上限,可以用下式表示:
-
对任意a>0,Var(X)为X的方差,定义如下:
-
若以马尔可夫不等式为基础,切比雪夫不等式可视为考虑以下随机变量
-
根据马尔可夫不等式,可得到以下的结果
-
矩阵形式的马尔可夫不等式
令 为自共轭矩阵形式的随机变量,且 ,则
-
应用实例
- 马尔可夫不等式可用来证明切比雪夫不等式。
- 马尔可夫不等式可用来证明一个非负的随机变量,其平均值 和中位数 满足 的关系。
参见
参考资料
- ^ Sheldon M Ross. Introduction to probability and statistics for engineers and scientists. Academic Press. 2009: 第127页. ISBN 9780123704832.
- ^ E.M. Stein, R. Shakarchi, "Real Analysis, Measure Theory, Integration, & Hilbert Spaces", vol. 3, 1st ed., 2005, p.91