简介
若函数 表示一个未知的密度,对 做拉东变换,相当于得到 投影后的讯号,举例来说: 相当于人体组织,断层扫描的输出讯号相当于经过拉东变换的 。
因此,可以用拉东反变换从投影后的密度函数,重建原始的密度函数,它也是重建断层扫描的数学理论基础,另一个被广为人知名词的是三维重建。
拉东变换后的讯号称作正弦图(sinogram),因为一个偏离中心的点的拉东变换是一条正弦曲线。所以对一些小点的拉东变换,会看起来像很多不同振福、相位的正弦函数重叠在一起。
拉东变换可以应用在:X射线电脑断层扫描、条码扫描器、macromolecular assemblies的电子显微镜例如:病毒、Reflection seismology、蛋白质复合体,而且也是双曲线偏微分方程的解。
定义
令密度函数 是一个的定义域为 的紧支撑。令 为拉东变换的运算子(operator),则 是一个定义在
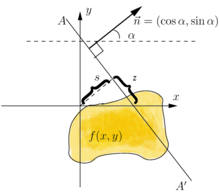
空间中的直线 ,它的定义如下
-
可以把直线 改写成一个弧长 的参数式
-
是直线 和原点的距离,而 是垂直于 的法线和 轴的夹角,
接下来,我们可以令 当作 平面上的新坐标系统,把这个坐标变换带入到拉东变换得到
-
更进一步,我们可以把 推广到 的欧几里得空间,对一个紧支撑的连续函数 做拉东变换后的函数 是定义在
的超平面上,
-
积分的对象是自然超平面测度(natural hypersurface measure),而 是原本的 的高维推广。可以观察到对 里的任意元素,
都是某个轨迹方程式的解
-
而 是一个单位向量且属于 , ,n维的拉东变换可以改写成定义在 上的函数
-
也可以借由其他方式将拉东变换推广,也就是对 的k维仿射子空间作(k-dimensional affine subspaces)积分。
而这种推广拉东变换的特殊情况被广泛应用在X射线电脑断层扫描,他的做法是对一条直线积分。
与傅里叶变换的关系
主条目:Projection-slice theorem
拉东变换和傅里叶变换之间有很强的关联性。单变量的傅里叶变换的定义是
-
而双变量 的傅里叶变换是
-
把拉东变换的运算子的表记从 改成 。根据Projection-slice theorem学说,
-
因此一个初始函数沿着一条线倾角 的二维的傅里叶变换,相当于对拉东变换做一维的傅里叶变换。这个结果可以推广到n维
-
对偶变换
对偶拉东变换是拉东变换的埃尔米特伴随。令在空间 上的函数 ,而对偶拉东变换的运算子定义为 。作用在 上
-
积分的范围是所有和 相交的超平面集合,而测度(measure) 是集合 特殊的概率测度(Probability measure),
当对着 旋转时, 的值不会改变
对于一个二维的拉东变换,其对偶变换是
-
在影像处理的文章中,对偶变换经常被称作反向传播算法(back propagation) [2],
因为
交结性质
根据拉普拉斯算子 在 的定义是
-
这是一个旋转不变性的二阶微分算子,在空间 ,半径的二阶导数
-
也是旋转不变性。
而拉东变换与其对偶变换属于交结运算子(intertwining operator),是因为
-
重建方法
重建处理是指从投影影像重建一个影像,或是一个函数 。重建处理是一种逆问题(inverse problem)。
拉东反变换公式
对于二维拉东变换,最常被使用的解析公式(analytical formula) ,是Filtered Backprojection Formula或拉东反变换公式,反变换公式为
- [3]
函数 满足 [4],卷积核 (convolution kernel) 在一些文章中称作Ramp filter。
不适定问题 (ill-posedness)
直觉上,反变换公式应该和微分类似, 。我们可以看的出来反变换公式
的行为类似微分。大致上来说,这个反变换公式把目标奇异化(singular);要如何量化拉东反转化的不适定问题 (ill-posedness)呢?首先可以写出
-
即是前面定义的反变换运算子,且伴随着(adjoint to)拉东变换,因此 ,上式变成
-
复数指数函数 ,是 的本征函数 (eigenfunction) ,
而特征值 (eigenvalue)为 。 的奇异值 (singular values) 是 ,
因为这些奇异值 (singular values)会趋近于0,所以 是无界的(unbounded) [4]。
反变换公式
外显(explicit)且计算效率好的拉东反变换公式,以及他的对偶是存在的。n维的反拉东变换可以由[5]
-
其中
-
而 是拉普拉斯算子(Laplacian), 是伪微分算子(pseudodifferential operator)
-
是傅里叶变换的运算子(operator)。
参见
- 反卷积
- X-ray变换
- Funk变换
- 霍夫变换
- 迭代稀疏渐近最小方差算法
注释
参考
- Deans, Stanley R., The Radon Transform and Some of Its Applications, New York: John Wiley & Sons, 1983 .
- Helgason, Sigurdur, Geometric analysis on symmetric spaces, Mathematical Surveys and Monographs 39 2nd, Providence, R.I.: American Mathematical Society, 2008, ISBN 978-0-8218-4530-1, MR 2463854 .
- Helgason, Sigurdur, Groups and Geometric Analysis: Integral Geometry, Invariant Differential Operators, and Spherical Functions, Academic Press, 1984, ISBN 0-12-338301-3 .
- Herman, Gabor T., Fundamentals of Computerized Tomography: Image Reconstruction from Projections 2nd, Springer, 2009, ISBN 978-1-85233-617-2 .
- Minlos, R.A., Radon transform, Hazewinkel, Michiel (编), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 .
- Natterer, Frank, The Mathematics of Computerized Tomography, Classics in Applied Mathematics 32, Society for Industrial and Applied Mathematics, ISBN 0-89871-493-1
- Natterer, Frank; Wübbeling, Frank, Mathematical Methods in Image Reconstruction, Society for Industrial and Applied Mathematics, ISBN 0-89871-472-9 .
- Radon, Johann, Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten, Berichte über die Verhandlungen der Königlich-Sächsischen Akademie der Wissenschaften zu Leipzig, Mathematisch-Physische Klasse [Reports on the proceedings of the Royal Saxonian Academy of Sciences at Leipzig, mathematical and physical section] (Leipzig: Teubner), 1917, (69): 262–277 ; Translation: Radon, J.; Parks, P.C. (translator), On the determination of functions from their integral values along certain manifolds, IEEE Transactions on Medical Imaging, 1986, 5 (4): 170–176, PMID 18244009, doi:10.1109/TMI.1986.4307775 .
- Roerdink, J.B.T.M., Tomography, Hazewinkel, Michiel (编), 数学百科全书, Springer, 2001, ISBN 978-1-55608-010-4 .
- 埃里克·韦斯坦因. 拉東變換. MathWorld. .