几何级数

提示：此条目的主题不是等比数列。

在数学中，几何级数（英语：Geometric series）是无穷多个项的总和，这些连续项之间的公比是恒定的。例如，该数列

${\displaystyle {\frac {1}{2}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{16}}\,+\,\cdots }$

是无穷级数最简单的例子之一，可以作为泰勒级数和傅立叶级数的基本介绍。

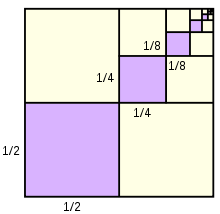
几何级数1/4 + 1/16 + 1/64 + 1/256 + ... 面积用紫色表示，其总和为正方形面积的三分之一

几何级数在微积分的早期发展中起到了重要作用，在整个数学中都有使用，并且在物理学、工程学、生物学、经济学、计算机科学和金融学中都有重要的应用。

级数和数列的区别在于数列强调数字以排列形式出现，而级数是强调该数列的总和。