基本定义
双极圆柱坐标 通常定义为
- 、
- 、
- ;
其中,点 的 坐标等于 的弧度, 坐标等于 与 的比例的自然对数
- 。
注意到焦线 与 的坐标分别为 与 。
坐标曲面
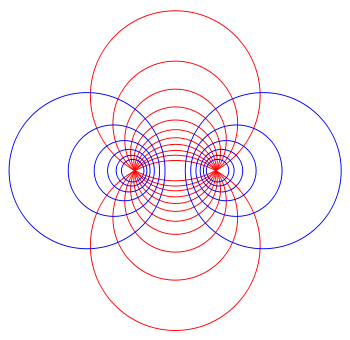
双极坐标的几何诠释。
与
的夹角
的弧度是
。
与
的比例的
自然对数是
。
与
的等值曲线都是圆圈,分别以红色与蓝色表示。两条等值曲线以直角相交(以洋红色表示)。
不同 的坐标曲面是一组不同圆心线,而相交于两个焦线 与 的圆柱面:
- 。
它们的圆心线都包含于 yz-平面。正值 的圆柱面的圆心线都在 半空间;而负值 的圆柱面的圆心线则在 半空间。当绝对值 增加时,圆半径会减小,圆心线会靠近原点。当圆心线包含原点时, 达到最大值 。
不同 的坐标曲面是一组围着焦线,互不相交,不同半径的圆柱面。半径为
- 。
它们的圆心线都包含于 xz-平面。正值 的圆柱面在 半空间;而负值 的圆柱面在 半空间。 平面则与 yz-平面同平面。当 值增加时,圆柱面的半径会减少,圆心线会靠近焦点。
逆变换
双极圆柱坐标 可以用直角坐标 来表示。点 P 与两个焦线之间的距离是
- 、
- 。
是 与 的比例的自然对数:
- 。
是两条从点 P 到两个焦点的线段 与 的夹角。这夹角的弧度是 。用余弦定理来计算:
- 。
z-坐标的公式不变:
- 。
标度因子
双极圆柱坐标 与 的标度因子相等;而 的标度因子是 1 :
- 、
- 。
所以,无穷小体积元素等于
- 。
拉普拉斯算子是
- 。
其它微分算子,例如 与 ,都可以用双极圆柱坐标表达,只需要将标度因子代入正交坐标系的一般方程式内。
应用
双极圆柱坐标有一个经典的应用,这是在解析像拉普拉斯方程或亥姆霍兹方程这类的偏微分方程式。在这些方程式里,双极圆柱坐标允许分离变数法的使用。一个典型的例题是,有两个互相平行的圆柱导体,请问其周围的电场为什么?应用双极圆柱坐标,我们可以精致地分析这例题。
参阅
参考文献
- Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: pp. 187–190.
- Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 182. ASIN B0000CKZX7.
- Moon P, Spencer DE. Conical Coordinates (r, θ, λ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: unknown. ISBN 978-0387184302.