棱柱
棱柱是几何学中的一种常见的三维多面体,指平面上的一个多边形平行投影到与该平面平行的平面所截得的封闭几何体。棱柱的两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都相互平行。
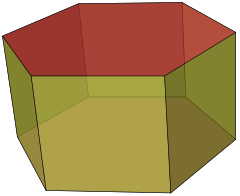 以六角柱为例 | |||
| 类别 | 棱柱 | ||
|---|---|---|---|
| 对偶多面体 | 双n角锥 | ||
| 数学表示法 | |||
| 考克斯特符号 | |||
| 施莱夫利符号 | {n}×{} or t{2, n} | ||
| 性质 | |||
| 面 | |||
| 边 | |||
| 顶点 | |||
| 欧拉特征数 | F=, E=, V= (χ=2) | ||
| 组成与布局 | |||
| 面的种类 | 多边形 矩形 | ||
| 顶点图 | 4.4.n | ||
| 对称性 | |||
| 对称群 | Dnh, [n,2], (*n22), order 4n | ||
| 旋转对称群 | Dn, [n,2]+, (n22), order 2n | ||
| 特性 | |||
| 凸、semi-regular、点可递 | |||
| 图像 | |||
| |||
| 注:为底面边数 。 | |||
若用于截平行平面的平面数为n,那么该棱柱便称为n-棱柱。如三棱柱就是由两个平行的平面被三个平面所垂直截得的封闭几何体。
棱柱的各种属性
底面
棱柱中两个互相平行的面,叫做棱柱的底面。 并且底面与侧面互相垂直。
侧面
棱柱中除两个底面以外的其余各个面都叫做棱柱的侧面。
侧棱
棱柱中两个侧面的公共边叫做棱柱侧棱。
顶点
棱柱中侧面与底面的公共顶点叫做棱柱的顶点。
对角线
棱柱中不在同一平面上的两个顶点的连线叫做棱柱的对角线。
高
棱柱的两个底面的距离叫做棱柱的高。
对角面
棱柱中过不相邻的两条侧棱的截面叫做棱柱的对角面。
体积
假设一个棱柱的底面面积为 ,高为 ,那么这个棱柱的体积为:
一些特殊的棱柱
斜棱柱
侧棱不垂直于底面的棱柱叫做斜棱柱,画斜棱柱时,一般将侧棱画成不与底面垂直。
直棱柱
侧棱垂直于底面的棱柱叫做直棱柱。画直棱柱时,应将侧棱画成与底面垂直。
正棱柱
底面是正多边形的直棱柱叫做正棱柱。[1]
参见
外部链接
参考文献
- ^ 周筱亭; 黄敏晃. 第二章第七節 柱體與錐體. 國小數學教材分析:幾何. 台北县: 国立教育研究院筹备处. 2006年 [2020-11-05]. ISBN 986-00-4770-7. 原始内容存档于2020-11-05 (中文).