蝴蝶定理(Butterfly theorem),是古典欧氏平面几何的最精彩的结果之一。蝴蝶定理最先是作为一个征求证明的问题,这个命题最早出现在1815年,而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号,题目的几何图形象一只蝴蝶,便以此命名。这个定理的证法多得不胜枚举,至今仍然被数学热爱者研究,在考试中时有出现各种变形。
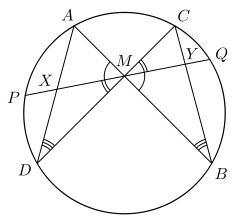
最基本的叙述为:设M为圆内弦PQ的中点,过M作弦AB和CD。设AD和BC各相交PQ于点X和Y,则M是XY的中点。
这个命题最早作为一个征解问题出现在公元1815年英国的一本杂志《男士日记》(Gentleman's Diary)39-40页上。登出的当年,英国一个自学成才的中学数学教师W.G.霍纳(他发明了多项式方程近似根的霍纳法)给出了第一个证明,完全是初等的;另一个证明由理查德·泰勒(Richard Taylor)给出。一种早期的证明由M.布兰德(Miles Bland)在《几何问题》(1827年)一书中给出。最为简洁的证法是射影几何的证法,由英国的J·开世在"A Sequel to the First Six Books of the Elements of Euclid"(中译:近世几何学初编,李俨译,上海商务印书馆 1956 )给出,只有一句话,用的是线束的交比。1981年,Crux杂志刊登了K.萨蒂亚纳拉亚纳(Kesirajn Satyanarayana)用解析几何的一种比较简单的方法(利用直线束,二次曲线束)。
该定理实际上是射影几何中一个定理的特殊情况,有多种推广:
- M,作为圆内弦是不必要的,可以移到圆外。
- 圆可以改为任意圆锥曲线。
- 将圆变为一个完全四角形,M为对角线交点。
- 去掉中点的条件,结论变为一个一般关于有向线段的比例式,称为“坎迪定理”,
 不为中点时满足:
不为中点时满足:  ,这对2,3均成立。
,这对2,3均成立。
从 向 和 作垂线,设垂足分别为 和 。类似地,从 向 和 作垂线,设垂足分别为 和 。
现在,由于
-
-
-
-
-
-
-
-
从这些等式,可以很容易看出:
-
-
-
-
由于 =
现在,
-
因此,我们得出结论:
,也就是说, 是 的中点。
证毕。