 提示
提示:此条目的主题不是
圆心角。
此条目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证实。 (2017年2月25日)
请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 |
在几何学中,当圆的两条割线在圆上相遇时,就会形成圆周角。
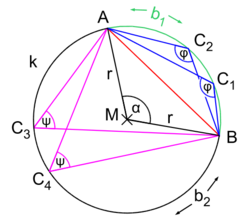
圆周角C
1与C
2相等,C
3与C
4相等。同时C
3的大小为圆心角α的一半。
一般来说,圆周角可被视为共用一个端点的两条弦。
历史
圆周角的基本性质记载于《几何原本》第三卷的第20至22号命题。几何原本中的命题为:
- 圆周角大小为对同弧的圆心角一半
- 对同弧的圆周角等
- 共用一弦的两圆周角大小和为180°
定理
- 圆周角大小为对同圆弧的圆心角的½
- 同弧的圆周角相等或互补
- 若两圆周角定点在弦所在直线的同一边, 则两圆周角相等
- 若两圆周角定点分别在弦所在直线的两边, 则圆周角互补
- 若两圆周角定点在一条直径上, 则圆周角恒等于90°[1]
参考资料