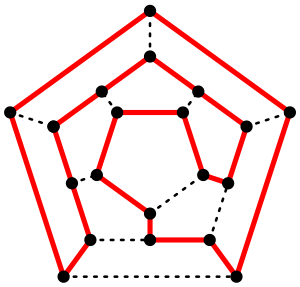
哈密顿路径问题

哈密顿环问题与哈密顿路径问题之间有着很简单的关系：

• 给定图${\displaystyle G}$  ,通过加入新顶点${\displaystyle v}$  并将新顶点与所有其他顶点连接起来，我们得到了图${\displaystyle H}$ 。 在图${\displaystyle G}$  之上的哈密顿路径问题与在${\displaystyle H}$ 之上的哈密顿环问题等价。因此寻找哈密顿路径的速度不可能比寻找哈密顿环的速度快很多。
• 从另一个方向来看，给定图${\displaystyle G}$ ，给定图上一个顶点${\displaystyle v}$ ，通过加入新顶点给定图${\displaystyle v'}$ ,并且让${\displaystyle v'}$ 的邻居等于${\displaystyle v}$ 的邻居，再增加两个度为1的新顶点，并让他们分别与${\displaystyle v}$ 和${\displaystyle v'}$ 相连，得到图${\displaystyle H}$ ，则图${\displaystyle G}$ 上的哈密顿环问题与图${\displaystyle H}$ 上的哈密顿路径问题等价。^[2]

在一个阶数为${\displaystyle n}$ 的图中，可能成为哈密顿路径的顶点序列最多有有${\displaystyle n}$ !个（在完全图的情况下恰好为${\displaystyle n}$ !个)，因此暴力搜索所有可能的顶点序列是非常慢的。 一个早期的在有向图上寻找哈密顿环的算法是Martello的枚举算法^[3] 由Frank Rubin^[4] 提供的搜索过程将图的边分为3种类型：必须在路径上的边，不能在路径上的边，和未定边。在搜索的过程中，一个决策规则的集合将未定边进行分类，并且决定是否继续进行搜索。这个算法将图分成几个部分，在它们上问题能够被单独地解决。

另外，Bellman, Held, and Karp 的动态规划 算法可以在O(n² 2ⁿ)时间内解决问题。在这个方法中，对每个顶点集${\displaystyle S}$ 和其中的每一个顶点${\displaystyle v}$  ，均做出如下的判定：是否有一条经过${\displaystyle S}$ 中每个顶点，并且在${\displaystyle v}$ 结束的路径，对于每一对${\displaystyle S}$ 和${\displaystyle v}$ ，当且仅当存在${\displaystyle v}$ 的邻居${\displaystyle w}$ 满足存在一条路径经过${\displaystyle S-v}$ 的所有顶点，并在${\displaystyle w}$ 上结束的路径时，存在路径经过${\displaystyle S}$ 中每个顶点，并且在${\displaystyle v}$ 结束。这个充要条件已经可以之前的动态规划计算中确认。^[5][6]

Andreas Björklund通过inclusion–exclusion principle将哈密尔顿环的计数问题规约成一个更简单，圈覆盖的计数问题，后者可以被通过计算某些矩阵的行列式解决。通过这个方法，并通过蒙特卡洛算法，对任意 ${\displaystyle n}$ 阶图，可以在O(1.657ⁿ)时间内解决。对于二分图，这个算法可以被进一步提升至o(1.415ⁿ).^[7]

对于最大度小于等于3的图，一个回溯搜索的方法可以在 O(1.251ⁿ)时间内找到哈密顿环.^[8]

哈密顿环和哈密顿路径也可以通过SAT solver找到.

哈密顿环和哈密顿路径问题是FNP问题，它的决定性问题 是检测是否存在一条哈密顿环或哈密顿路径。有向图和无向图上的哈密顿环问题是 卡普的二十一个NP-完全问题中的其中两个。对于一些特殊类型的图来说，它们仍然是NP完全的。例如：

• 二分图,^[9]
• 最大度为3的无向平面图,^[10]
• 入度和出度最大为2的有向平面图,^[11]
• 无桥的无向的平面3-正则二分图，
• 3-顶点连通，3-正则的二分图，^[12]
• square grid graph的子图,^[13]
• square grid graph的3-正则子图.^[14]

然而，对于某些类型的图，哈密顿环和哈密顿路径问题可以在多项式时间内解决：

• 根据Tutte的结论，4-顶点连通 平面图总是存在哈密顿环，并且可以在线性时间内找到哈密顿环。^[15] by computing a so-called Tutte path.
• Tutte通过证明2-正则平面图包含Tutte路径，证明了以上的结论。对2-正则平面图来说，其Tutte路径可以在平方时间内找到，^[16], 这可能可以被用来寻找一般平面图上的哈密顿环和较长的环。

将以上提供的条件汇总起来，3-正则，3-定点连通的二分图是否总是存在哈密顿环这一问题仍然是开放的,在这个情况下这一问题不是NP完全的，详见 Barnette's conjecture.

在所有顶点的度都是奇数的途中，一个与握手引理有关的结论说明对于任意一条边来说，经过它的哈密顿环的个数总是偶数，因此如果存在一条哈密顿环，则一定存在另一条 ^[17] 然而，找到第二条哈密顿换并不是一个简单的计算问题。Papadimitriou定义了一个 复杂性类复杂性类 PPA来描述这一类问题。 ^[18]

• Hamiltonian Page : Hamiltonian cycle and path problems, their generalizations and variations

1. ^ Michael R. Garey and David S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, 1979, ISBN 978-0-7167-1045-5  A1.3: GT37–39, pp. 199–200.
2. ^ Reduction from Hamiltonian cycle to Hamiltonian path
3. ^ Martello, Silvano, An Enumerative Algorithm for Finding Hamiltonian Circuits in a Directed Graph, ACM Transactions on Mathematical Software, 1983, 9 (1): 131–138, doi:10.1145/356022.356030 
4. ^ Rubin, Frank, A Search Procedure for Hamilton Paths and Circuits, Journal of the ACM, 1974, 21 (4): 576–80, doi:10.1145/321850.321854 
5. ^ Bellman, R., Dynamic programming treatment of the travelling salesman problem, Journal of the ACM, 1962, 9: 61–63, doi:10.1145/321105.321111 .
6. ^ Held, M.; Karp, R. M., A dynamic programming approach to sequencing problems (PDF), J. SIAM, 1962, 10 (1): 196–210 [2020-10-03], doi:10.1137/0110015, hdl:10338.dmlcz/103900, （原始内容存档 (PDF)于2019-09-22） .
7. ^ Björklund, Andreas, Determinant sums for undirected Hamiltonicity, Proc. 51st IEEE Symposium on Foundations of Computer Science (FOCS '10): 173–182, 2010, ISBN 978-1-4244-8525-3, arXiv:1008.0541  , doi:10.1109/FOCS.2010.24 .
8. ^ Iwama, Kazuo; Nakashima, Takuya, An improved exact algorithm for cubic graph TSP, Proc. 13th Annual International Conference on Computing and Combinatorics (COCOON 2007), Lecture Notes in Computer Science 4598: 108–117, 2007, ISBN 978-3-540-73544-1, doi:10.1007/978-3-540-73545-8_13 .
9. ^ Proof that the existence of a Hamilton Path in a bipartite graph is NP-complete. Computer Science Stack Exchange. [2019-03-18]. 
10. ^ Garey, M. R.; Johnson, D. S.; Stockmeyer, L., Some simplified NP-complete problems, Proc. 6th ACM Symposium on Theory of Computing (STOC '74): 47–63, 1974, doi:10.1145/800119.803884 .
11. ^ Plesńik, J., The NP-completeness of the Hamiltonian cycle problem in planar digraphs with degree bound two (PDF), Information Processing Letters, 1979, 8 (4): 199–201 [2020-10-03], doi:10.1016/0020-0190(79)90023-1, （原始内容存档 (PDF)于2020-11-25） .
12. ^ Akiyama, Takanori; Nishizeki, Takao; Saito, Nobuji, NP-completeness of the Hamiltonian cycle problem for bipartite graphs, Journal of Information Processing, 1980–1981, 3 (2): 73–76, MR 0596313 .
13. ^ Itai, Alon; Papadimitriou, Christos; Szwarcfiter, Jayme, Hamilton Paths in Grid Graphs, SIAM Journal on Computing, 1982, 4 (11): 676–686, doi:10.1137/0211056 .
14. ^ Buro, Michael, Simple Amazons endgames and their connection to Hamilton circuits in cubic subgrid graphs (PDF), Conference on Computers and Games, Lecture Notes in Computer Science 2063: 250–261, 2000 [2020-10-03], ISBN 978-3-540-43080-3, doi:10.1007/3-540-45579-5_17, （原始内容存档 (PDF)于2020-11-06） .
15. ^ Chiba, Norishige; Nishizeki, Takao, The Hamiltonian cycle problem is linear-time solvable for 4-connected planar graphs, Journal of Algorithms, 1989, 10 (2): 187–211, doi:10.1016/0196-6774(89)90012-6 
16. ^ Schmid, Andreas; Schmidt, Jens M., Computing Tutte Paths, Proceedings of the 45th International Colloquium on Automata, Languages and Programming (ICALP'18), to appear., 2018 
17. ^ Thomason, A. G., Hamiltonian cycles and uniquely edge colourable graphs, Advances in Graph Theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977), Annals of Discrete Mathematics 3: 259–268, 1978, ISBN 9780720408430, MR 0499124, doi:10.1016/S0167-5060(08)70511-9 .
18. ^ Papadimitriou, Christos H., On the complexity of the parity argument and other inefficient proofs of existence, Journal of Computer and System Sciences, 1994, 48 (3): 498–532, MR 1279412, doi:10.1016/S0022-0000(05)80063-7 .