抛物线坐标系(英语:Parabolic coordinates)是一种二维正交坐标系,两个坐标的等值曲线都是共焦的抛物线。将二维的抛物线坐标系绕着抛物线的对称轴旋转,则可以得到三维的抛物线坐标系。
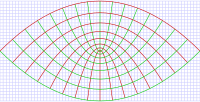
抛物线坐标系的绿色的

等值曲线和红色的

等值曲线。横轴与纵轴分别为 x-轴与 y-轴。
实际上,抛物线坐标可以应用在许多物理问题。例如,斯塔克效应(Stark effect),物体边缘的位势论,以及拉普拉斯-龙格-冷次向量的保守性。
二维抛物线坐标系
直角坐标 可以用二维抛物线坐标 表示为
- 、
- ;
其中, , 。
反算回来,二维抛物线坐标 可以用直角坐标 表示为
- 、
- 。
坐标 为常数的曲线形成共焦的,凹性向上的(往 +y-轴)抛物线:
- ,
而坐标 为常数的曲线形成共焦的,凹性向下的(往 -y-轴)抛物线:
- 。
这些抛物线的焦点的位置都在原点。
二维标度因子
抛物线坐标 的标度因子相等:
- 。
因此,面积的无穷小元素是
- 。
拉普拉斯算子是
- 。
其它微分算子,像 , ,都可以用 坐标表示,只要将标度因子代入在正交坐标系条目内的一般公式。
三维抛物线坐标系
三维抛物线坐标的
坐标曲面。红色的抛物曲面的坐标
。蓝色的抛物曲面的坐标
。黄色的半平面的坐标
。三个面相交于点
(以黑色小球表示)。
将二维的抛物线坐标系绕着抛物线的对称轴旋转,则可以得到三维的抛物线坐标系,又称为旋转抛物线坐标系。将对称轴与 z-轴排列成同直线;而抛物线坐标系的共焦点与直角坐标系的原点同地点。直角坐标 可以用三维抛物线坐标 表示为
- 、
- 、
- ;
其中, , ,方位角 定义为
- 。
反算回来,三维抛物线坐标 可以用直角坐标 表示为
- 、
- 、
- 。
每一个 -坐标曲面都是共焦的,凹性向上的(往 +z-轴)抛物曲面:
- ,
而每一个 >-坐标曲面都是共焦的,凹性向下的(往 -z-轴)抛物曲面:
- 。
这些抛物曲面的焦点的位置都在原点。
三维标度因子
三维标度因子为:
- 、
- 、
- 。
我们可以观察出,标度因子 , 与二维标度因子相同。因此,体积的无穷小元素是
- 。
拉普拉斯算子是
- 。
其它微分算子,像 , ,都可以用 坐标表示,只要将标度因子代入在正交坐标系 条目内的一般公式。
第二种表述
另外还有一种抛物线坐标系的表述,专门用于哈密顿-亚可比方程式。假若使用此种表述的公式,则哈密顿-亚可比方程式可以很容易的分解出来。应用此方法,可以导引出拉普拉斯-龙格-冷次向量的恒定性.
采用下述从抛物线坐标变换至直角坐标的公式:
- 、
- 、
- 。
假若 ,则可得到一片截面;其坐标被限制于 的 +xz-半平面:
- 、
- 。
假若包含于一条曲线的每一点的坐标 是一个常数, ,则
- 。
这是一个共焦点在原点的抛物线;对称轴与 z-轴同轴;凹性向上。
假若包含于一条曲线的每一点的坐标 是一个常数, ,则
- 。
这也是一个共焦点在原点的抛物线;对称轴与 z-轴同轴;凹性向下。
思考任何一条向上的抛物线 与任何一条向下的抛物线 ,我们想要求得两条曲线的相交点:
- 。
稍微计算,可得
- 。
将相交点的横坐标 代入向上的抛物线的公式,
- 。
所以,相交点 P 坐标为 。
思考正切这两条抛物线于点 P 的一对切线。向上的抛物线的切线的斜率为
- 。
向下的抛物线的切线的斜率为
- 。
两个斜率的乘积为
- 。
所以,两条切线相垂直。对于任何两条凹性相反的抛物线,都会有同样的结果。
假设 。让 值从 缓慢增值,这半平面会相应地绕着 z-轴按照右手定则旋转;抛物线坐标为常数的抛物线 形成了抛物曲面。一对相反的抛物曲面的相交 设定了一个圆圈。而 值设定的半平面,切过这圆圈于一个唯一点。这唯一点的直角坐标是[1]:
- 、
- 、
- 。
参考文献
- Morse PM, Feshbach H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill. 1953: p. 660. )
- Margenau H, Murphy GM. The Mathematics of Physics and Chemistry. New York: D. van Nostrand. 1956: pp. 185–186.
- Korn GA, Korn TM. Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. 1961: p. 180.
- Sauer R, Szabó I. Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. 1967: p. 96.
- Zwillinger D. Handbook of Integration. Boston, MA: Jones and Bartlett. 1992: p. 114. ISBN 0-86720-293-9.
- Moon P, Spencer DE. Parabolic Coordinates (μ, ν, ψ). Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions corrected 2nd ed., 3rd print ed. New York: Springer-Verlag. 1988: pp. 34–36 (Table 1.08). ISBN 978-0387184302.
- ^ Menzel, Donald H. Mathematical Physics. United States of America: Dover Publications. 1961: pp. 139. ISBN 978-0486600567 (英语).


