截角六阶八边形镶嵌
在几何学中,截角六阶八边形镶嵌是一种双曲半正镶嵌。 每个顶点皆由一个正六角形与两个正十六边形构成。在施莱夫利符号中用t{8,6}来表示。
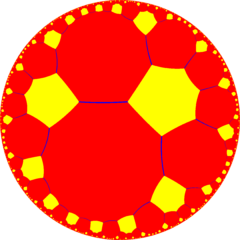 庞加莱圆盘模型 | ||
| 类别 | 双曲半正镶嵌 | |
|---|---|---|
| 对偶多面体 | 六角化八阶六边形镶嵌 | |
| 数学表示法 | ||
| 考克斯特符号 | ||
| 施莱夫利符号 | t{8,6} 2t{6.8} | |
| 威佐夫符号 | 6 | 8 2 | |
| 组成与布局 | ||
| 顶点图 | 6.16.16 | |
| 对称性 | ||
| 对称群 | [8,6], (*862) | |
| 旋转对称群 | [8,6]+, (862) | |
| 图像 | ||
| ||
半正涂色
截角六阶八边形镶嵌的另一个构造的施莱夫利符号为t{(8,8,3)},又被称为 截角三阶双八边形镶嵌镶嵌:
对称性
该镶嵌的对偶表示著[(8,8,3)] (*883) 对称性的基本域。3个子群对称性可透过去除以及交替[(8,8,3)]的镜射线以构成。 在这些图像中,基本域由白色和黑色交替着色,镜射线则存在于色块之间的边界上。
通过添加一条将基本域平分的镜子镜射线,对称性可以增倍成862对称性。
相关多面体与镶嵌
| 八阶六边形镶嵌 | ||||||
|---|---|---|---|---|---|---|
| 对称性:[8,6], (*862) | ||||||
| {8,6} | t{8,6} |
r{8,6} | 2t{8,6}=t{6,8} | 2r{8,6}={6,8} | rr{8,6} | tr{8,6} |
| 对偶 | ||||||
| V86 | V6.16.16 | V(6.8)2 | V8.12.12 | V68 | V4.6.4.8 | V4.12.16 |
| 交错 | ||||||
| [1+,8,6] (*466) |
[8+,6] (8*3) |
[8,1+,6] (*4232) |
[8,6+] (6*4) |
[8,6,1+] (*883) |
[(8,6,2+)] (2*43) |
[8,6]+ (862) |
| h{8,6} | s{8,6} | hr{8,6} | s{6,8} | h{6,8} | hrr{8,6} | sr{8,6} |
| 对偶 | ||||||
| V(4.6)6 | V3.3.8.3.8.3 | V(3.4.4.4)2 | V3.4.3.4.3.6 | V(3.8)8 | V3.45 | V3.3.6.3.8 |
参见
参考资料
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 0-486-40919-8. LCCN 99035678.
外部链接
- 埃里克·韦斯坦因. Hyperbolic tiling. MathWorld.
- 埃里克·韦斯坦因. Poincaré hyperbolic disk. MathWorld.
- Hyperbolic and Spherical Tiling Gallery (页面存档备份,存于互联网档案馆)
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings (页面存档备份,存于互联网档案馆)
- Hyperbolic Planar Tessellations, Don Hatch (页面存档备份,存于互联网档案馆)
