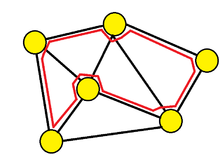
哈密顿路径

在图论中，哈密顿路径（台湾作汉米顿路径）是在无向图或有向图中，恰好能将图中所有顶点各拜访一次的路径。与之相近的概念为哈密顿环（台湾作汉米顿环），即该路径在拜访完图中所有顶点后会回到出发点，而构成一个环。要确定图中是否存在哈密顿路径或哈密顿环的问题称为哈密顿路径问题[1]，这个问题是一个NP完全的问题。哈密顿路径有时会跟尤拉路径一起讨论，因为哈密顿路径要求通过所有顶点（哈密顿路径问题）而尤拉路径要求通过所有边（一笔画问题）。[2]:218[3]

经过图中所有顶点的回路称为哈密顿环

定义

哈密顿路径是一个拜访过某图所有顶点的路径，且每个顶点只会被拜访一次。[4]存在哈密顿路径的图称为可追踪图。如果一个图中每对顶点都能找到一条哈密顿路径，则这个图可以被视为哈密顿连通的。哈密顿环或哈密顿回路是一个拜访过某图所有顶点的环或循环路径[5]:196，在这个循环路径中每个顶点只会被拜访一次，且拜访完所有顶点后会回到起始点。存在哈密顿环的图称为哈密顿图[6][7]。哈密顿环与哈密顿路径主要可以由起点和终点来区别：若一哈密顿路径起点与终点相同，其为哈密顿环；而若起点与终点不同，则其就不是哈密顿环，仅能视为哈密顿路径。[8]

哈密顿分解（英语：Hamiltonian decomposition）是将图分解成哈密顿环的边分解方式。[9]

哈密顿迷宫是一种逻辑益智游戏，其目标在于找到图中唯一的哈密顿环。[10][11]

性质

任何哈密顿环都可以透过移除一条边来转换成哈密顿路径。然而哈密顿路径只有路径的2端点相邻时才有机会透过新增一条边来转换成哈密顿环。所有具备哈密顿环的图（即哈密顿图）都是双连通图；但双连通图不一定会存在哈密顿环（即双连通图不一定是哈密顿图，如佩特森图）。[12]

阶数为n（n=1,2,3...）的简单图中存在的哈密顿环的总数为0, 0, 2, 10, 58, 616, 9932, 333386, 25153932, 4548577688, ...（OEIS数列A124964）。[13]

参见

参考文献

  1. ^ 漢密頓路徑 Hamiltonian path. 资讯与通信术语辞典. 国家教育研究院. 2003年6月 [2021-09-03]. （原始内容存档于2021-09-03）. 
  2. ^ 高通量测序数据分析 (PDF). 兴邦二校. [2021-09-03]. （原始内容存档 (PDF)于2021-08-06）. 
  3. ^ 徐力行. 沒有數字的數學. 天下文化. 2003-09-16. ISBN 9789864171842 （中文（台湾））. 
  4. ^ 特殊路徑與迴路. ck.tp.edu.tw. [2021-09-03]. （原始内容存档于2019-10-30）. 
  5. ^ Skiena, Steven; Pemmaraju, Sriram. "Hamiltonian Cycles" §5.3.4 in. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Cambridge University Press. 1990: 196-198. ISBN 978-0521806862. 
  6. ^ Weisstein, Eric W. (编). Hamiltonian Cycle. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  7. ^ Weisstein, Eric W. (编). Hamiltonian Graph. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. （英语）. 
  8. ^ Hamilton Circuit. ntnu.edu.tw. [2021-09-03]. （原始内容存档于2021-09-03）. 
  9. ^ Bermond, J.-C., Hamiltonian decompositions of graphs, directed graphs and hypergraphs, Annals of Discrete Mathematics, 1978, 3: 21–28, ISBN 9780720408430, MR 0505807, doi:10.1016/S0167-5060(08)70494-1 
  10. ^ de Ruiter, Johan. Hamilton Mazes – The Beginner's Guide. 2017. 
  11. ^ Friedman, Erich. Hamiltonian Mazes. Erich's Puzzle Palace. 2009 [27 May 2017]. （原始内容存档于16 April 2016）. 
  12. ^ Weisstein, Eric W. (编). Biconnected Graph. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. [2021-09-03]. （原始内容存档于2018-01-15） （英语）. 
  13. ^ Sloane, N.J.A. (编). Sequence A124964 (Total counts of distinct (directed) Hamiltonian cycles for all simple graphs of order n.). The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. 

外部链接