帕普斯面积定理

给定任意三角形，其两个任意平行四边形连接到其任意两侧，该定理描述在第三侧产生平行四边形，使得第三个平行四边形的面积等于其他两个平行四边形的面积之和。

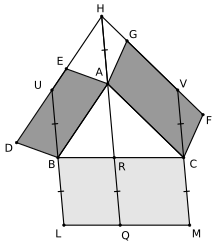
设${\displaystyle \Delta ABC\,}$ 为任意三角形，ABDE与ACFG是连接到三角形边AB与AC的两个任意平行四边形。延长的平行四边形边DE与FG在H点处相交。线段AH现在“变成”连接到三角形边BC的第三平行四边形BCLM的边，即在BC上产生线段BL与CM，使得BL与CM互相平行并且其长度等于AH。以下${\displaystyle A}$ 表示为平行四边形的面积：

${\displaystyle A_{ABDE}+A_{ACFG}=A_{BCLM}}$ 

该定理从两方面推广了毕氏定理。首先它适用于任意三角形，而不仅适用于直角三角形，其次它使用平行四边形而非正方形。对于任意三角形两侧的正方形，在第三侧产生相等面积的平行四边形，如果两侧为平行四边形直角的直角边，则第三侧（斜边）的平行四边形也是正方形。对于直角三角形，连接到直角腿的两个平行四边形在第三侧产生相等面积的矩形，并且如果两个平行四边形是正方形，那么第三侧上的矩形也将是正方形。

由于具有相同的基本长度与高度，平行四边形ABDE与ABUH具有相同的面积，相同的参数适用于平行四边形ACFG与ACVH、ABUH与BLQR、ACVH与RCMQ。 这已经产生了预期的结果，如下：

${\displaystyle {\begin{aligned}A_{ABDE}+A_{ACFG}\,{}&=A_{ABUH}+A_{ACVH}\\&=A_{BLRQ}+A_{RCMQ}\\&=A_{BCLM}\end{aligned}}}$ 

• Howard Eves. Pappus's Extension of the Pythagorean Theorem. The Mathematics Teacher. 1958-11, 51 (7): 544–546. JSTOR 27955752. （原始内容存档于2019-09-22）. 
• Howard Eves. Great Moments in Mathematics (before 1650). Mathematical Association of America. 1983: 37. ISBN 9780883853108. 
• Eli Maor（英语：Eli Maor）. The Pythagorean Theorem: A 4,000-year History. Princeton University Press. 2007: 58–59 [2022-02-16]. ISBN 9780691125268. （原始内容存档于2020-07-01）. 
• Claudi Alsina; Roger B. Nelsen. Charming Proofs: A Journey Into Elegant Mathematics. MAA. 2010: 77–78. ISBN 9780883853481. 

• The Pappus Area Theorem （页面存档备份，存于互联网档案馆）
• Pappus theorem （页面存档备份，存于互联网档案馆）