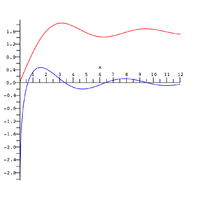
正弦积分
有两种不同的正弦积分:
-
-
是 的原函数,当 时为零; 是 的原函数,当 时为零。我们有:
-
注意到 是sinc函数,也是第零个球贝塞尔函数。
余弦积分
有两种不同的余弦积分:
-
-
-
其中 是欧拉-马斯刻若尼常数.
是 的原函数,当 时为零。我们有:
-
-
双曲正弦积分
主条目:双曲正弦积分函数
-
双曲余弦积分
主条目:Chi 函数
-
展开式
有各种各样的展开式,可以用于计算三角积分。
渐近展开式
-
-
这些级数是发散的,但可以用来估计,甚至是精确计算三角积分。
收敛级数
-
-
这些级数对于任何复数的 都是收敛的,但当 时,计算非常缓慢,也不是很精确。
与指数积分的关系
函数
-
称为指数积分,与正弦和余弦积分有以下的关系:
-
参见
参考文献
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 5)(页面存档备份,存于互联网档案馆)