相空间

约瑟夫·刘维尔首先于1838年在表述刘维定理的论文里涉及到相空间的概念，证实了相空间的体积守恒，但是他并不知道刘维定理可以应用于动力学问题。后来，卡尔·雅可比与路德维希·玻尔兹曼分别在发展力学理论与气体运动论时应用到相空间，并且引述了刘维定理的论文为参考文献。玻尔兹曼的学生保罗·埃伦费斯特在为一本1911年出版的百科全书撰写文章时，最先提出相空间这术语。^[1]

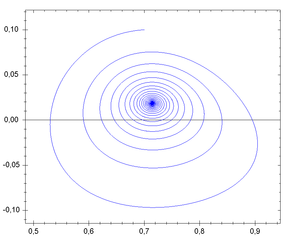
以力学系统来说，相空间通常是由位置变数以及动量变数所有可能值所组成。将位置变数与动量变数画成时间的函数有时称为相空间图，简称“相图”（phase diagram）。然而在物质科学（physical sciences）中，“相图”这词更常是留给一化学系统用以表示其热力学相态多种稳定性区域的图表，为压力、温度及化学组成等等之函数。

在一相空间中，系统的每个自由度或参数可以用多维空间中的一轴来代表。对于系统每个可能的状态，或系统参数值允许的组合，可以在多维空间描绘成一个点。通常这样的描绘点连接而成的线可以类比于系统状态随着时间的演化。最后相图可以代表系统可以存在的状态，而它的外型可以轻易地阐述系统的性质，这在其他的表示方法则不那么显明。一相空间可有非常多的维度。举例来说，一气体包含许多分子，每个分子在x、y、z方向上就要有3个维度给位置与3个维度给速度，可能还需要额外的维度给其他的性质。

在经典力学中，相空间坐标由广义坐标q_i以及其共轭的广义动量p_i所组成。研究由许多系统所构成的系综在此空间中的运动是属于经典统计力学的范畴。

1. ^ David D. Nolte. The tangled tale of phase space. Physics Today: 33–38. [2018-04-02]. doi:10.1063/1.3397041. （原始内容存档于2020-05-20）.