管状邻域

在数学中，一个光滑流形的子流形的管状邻域是它周围的一个开集，与法丛类似。

一个蓝色的曲线，和垂直于它的一些绿色的直线。直线在条带内的小部分为红色。

上图的近距离观察是这样。曲线是蓝色，它的管状邻域T是红色。用文章中的符号，曲线为S，包含曲线的空间为M，并且T=j(N).

法丛N的示意图，零截线N₀为蓝色。变换j将N₀映射到上图中的曲线S，将N映射到S的管状邻域。

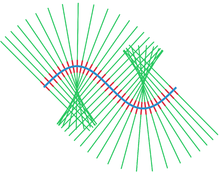
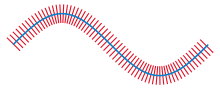
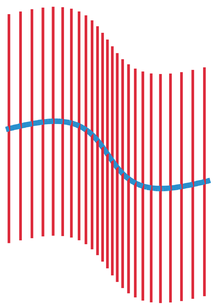
管状邻域的想法可以用一个简单的例子说明。考虑平面内一个没有自交的光滑曲线。在曲线的每一个点处作一条与这个曲线垂直的直线。这些直线之间会以一种很复杂的形式相交，除非这条曲线是直的。然而，如果只观察临近曲线的一个狭窄的条带，这些直线在条带内的部分不会相交，并会没有缝隙地覆盖这个条带。这个条带就是一个管状邻域。

一般地，令S为流形M的一个子流形，令N为在M上S的法丛。这里S扮演曲线的角色，M扮演包含曲线的空间的角色。考虑自然映射

${\displaystyle i:N_{0}\rightarrow S}$

建立起N的零截线N₀与M的一个子流形S之间的双射关系。关于值在M中的全部法丛N的这个映射的一个外延j，使j(N)是M上的一个开集，并且j是N与j(N)的一个同胚，称作管状邻域。