埃尔德什－莫德尔不等式

该不等式最早由埃尔德什在1935年在《美国数学月刊》上提出，作为第3740号问题。两年之后，由路易斯·莫德尔和D.F.巴罗证明。1957年，卡扎里诺夫提出了一个更简捷的证明^[1]。之后不断有更简洁、更基本的证明出现。1958年班考夫（Bankoff）给出了运用正交投影和相似三角形的证明，1997年和2004年出现了使用面积不等式的证明，1993年和2001年发现了根据托勒密定理的证明。

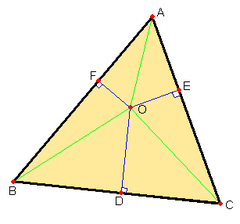
如右图，O为三角形ABC中的一个点。O到三角形三边的垂线分别交三条边于D、E、F。设线段${\displaystyle OA}$ 、${\displaystyle OB}$ 、${\displaystyle OC}$ 的长度分别是${\displaystyle x}$ 、${\displaystyle y}$ 、${\displaystyle z}$ ，线段${\displaystyle OD}$ 、${\displaystyle OE}$ 、${\displaystyle OF}$ 的长度分别是${\displaystyle p}$ 、${\displaystyle q}$ 、${\displaystyle r}$ ，那么埃尔德什-莫德尔不等式为：

一个初等的证明方式是使用三角函数以及均值不等式。

首先，由于${\displaystyle OF}$ 垂直于${\displaystyle AF}$ ，${\displaystyle OE}$ 垂直于${\displaystyle AE}$ ，A、F、O、E四点共圆且${\displaystyle OA}$ 为直径，因此线段${\displaystyle \displaystyle EF=OA\sin A=x\sin A}$ （角A为顶点A对应的内角）。

过点F、E作关于${\displaystyle BC}$ 的垂线交${\displaystyle BC}$ 于X、Y。过O作${\displaystyle BC}$ 的平行线分别交${\displaystyle FX}$ 、${\displaystyle EY}$ 于${\displaystyle U}$ 、${\displaystyle V}$ 。由于${\displaystyle OF}$ 垂直于${\displaystyle AF}$ ，${\displaystyle OE}$ 垂直于${\displaystyle AE}$ ，${\displaystyle \angle UFO=\angle B}$ ，${\displaystyle \angle VEO=\angle C}$ 。于是：

${\displaystyle UV=UO+OV=OF\sin \angle UFO+OE\sin \angle VEO=r\sin B+q\sin C}$ 

另一方面，注意到在直角梯形中${\displaystyle FUVE}$ 中，斜腰${\displaystyle EF}$ 的长度大于等于直角腰${\displaystyle UV}$ 。因此：

${\displaystyle x\sin A=EF\geq UV=r\sin B+q\sin C}$ 

${\displaystyle x\geq r{\frac {\sin B}{\sin A}}+q{\frac {\sin C}{\sin A}}}$ 

类似地，还有：

${\displaystyle y\geq r{\frac {\sin A}{\sin B}}+p{\frac {\sin C}{\sin B}}}$ ，${\displaystyle z\geq p{\frac {\sin B}{\sin C}}+q{\frac {\sin A}{\sin C}}}$ 

三式相加，得到：

${\displaystyle x+y+z\geq r\left({\frac {\sin B}{\sin A}}+{\frac {\sin A}{\sin B}}\right)+q\left({\frac {\sin C}{\sin A}}+{\frac {\sin A}{\sin C}}\right)+p\left({\frac {\sin C}{\sin B}}+{\frac {\sin B}{\sin C}}\right)}$ 

根据均值不等式，${\displaystyle \left({\frac {\sin B}{\sin A}}+{\frac {\sin A}{\sin B}}\right)\geq 2}$ ，等等，于是最终得到：

${\displaystyle x+y+z\geq 2(p+q+r)}$ 

这就是埃尔德什-莫德尔不等式。

从证明中可以看到，等号取得的充要条件是${\displaystyle \sin A=\sin B=\sin C}$ ，也就是说不等式中的等号成立当且仅当三角形是等边三角形。

1. ^ N.D.卡扎里诺夫，刘西垣 译. 几何不等式. 北京大学出版社. 1986年. 

• （英文）Claudi Alsina，Roger B. Nelsen. A Visual Proof of the Erd˝os-Mordell (PDF). InequalityForum Geometricorum，Volume 7 (2007) 99–102. [2009-10-28]. （原始内容存档 (PDF)于2020-06-05）. (埃尔德什-莫德尔不等式的历史和一个可视化证明)
• （英文）George Tsintsifas, Thessaloniki, Greece. The Erdos-Mordell inequality (PDF). 埃尔德什-莫德尔不等式的历史和若干个证明。
• O. Bottema (); et al. Geometric inequalities. Groningen, Wolters-Noordhoff. 1969.  引文格式1维护：显式使用等标签 (link)