重整化
重整化(Renormalization)是量子场论、统计场论和自相似几何结构中解决计算过程中出现无穷大的一系列方法。
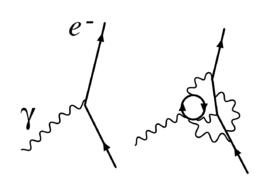
图1. 量子电动力学中的重整化:此例为简单的电子-光子交互作用,在一个重整化点决定了电子的电荷。实际上,可以在右图看到包含了在其他点更多复杂的交互作用。
在量子场论发展的早期,人们发现许多圈图(即微扰展开的高阶项)的计算结果含有发散(即无穷大)项。重整化是解决这个困难的一个方案。一个理论如果只有有限种发散项,则可以在拉格朗日量中引进有限数目的项来抵消这些无穷大项,这种情形被称为可重整。反之,如果理论中有无限种发散项,则称为不可重整。
可重整化曾被认为一个场论所必需满足的自洽性要求。它在量子电动力学和量子规范场论的发展过程中起过重要的作用。粒子物理的标准模型也是可重整的。
现代场论的观点认为所有理论都只是有效理论,它们都有它们的适用范围。除了所谓的终极理论,所有理论在原则上都是不可重整的。在这种观点下,重整化只是联系不同能标下理论的一种方法。
可重整化的理论
耦合的变化
例如:
的后两项发散.
为了消除发散,把积分下限分别改为无穷小的 和 ,这样积分就变成了
如果能保证 ,那么就可以得到
。
相关条目
- 正规化
- 重整化群(更多信息)
外部链接
参考文献
- ^ Mehra, Jagdish; Milton, Kimball A. Schwinger, Tomonaga, Feynman, and Dyson: the triumph of renormalization. Oxford University Press https://www.oxfordscholarship.com/view/10.1093/acprof:oso/9780198527459.001.0001/acprof-9780198527459-chapter-8. 2003-08-14 [2020-03-04]. ISBN 978-0-19-170959-3. doi:10.1093/acprof:oso/9780198527459.001.0001/acprof-9780198527459-chapter-8. (原始内容存档于2020-07-28) (美国英语). 缺少或
|title=为空 (帮助) - ^ Sin-Itiro Tomonaga Nobel Lecture. NobelPrize.org. 1966 [2020-03-04]. (原始内容存档于2021-04-21) (美国英语).
- ^ Schwinger. Renormalization theory of quantum electrodynamics (PDF). (原始内容存档 (PDF)于2020-03-04).
- ^ 'tHooft, G. Renormalization of massless Yang-Mills fields. Nuclear Physics B. 1971-10, 33 (1): 173–199 [2020-03-04]. doi:10.1016/0550-3213(71)90395-6. (原始内容存档于2021-04-21) (英语).