此条目没有列出任何参考或来源。 (2019年3月6日)
维基百科所有的内容都应该可供查证。请协助补充可靠来源以改善这篇条目。无法查证的内容可能会因为异议提出而移除。 |
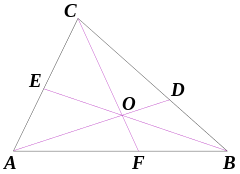
塞瓦线段是各顶点与其对边或对边延长线上的一点连接而成的直线段。塞瓦定理(英语:Ceva's theorem)指出:如果 的塞瓦线段AD 、BE、CF 通过同一点O,则
的塞瓦线段AD 、BE、CF 通过同一点O,则

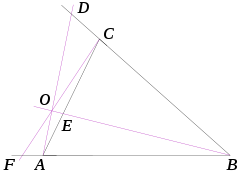
它的逆定理同样成立:若D、E、F分别在 的边BC、CA、AB或其延长线上(都在边上或有两点在延长线上),且满足
的边BC、CA、AB或其延长线上(都在边上或有两点在延长线上),且满足
 ,
,
则直线AD、BE、CF共点或彼此平行(于无限远处共点)。当AD、BE、CF中的任意两直线交于一点时,则三直线共点;当AD、BE、CF中的任意两直线平行时,则三直线平行。
它最先由意大利数学家乔瓦尼·塞瓦证明,因而得名。此定理又译西瓦定理或帅氏定理。
证明
-
由等比性质,
-
- 同理
-
证毕。
在三角形 ,角A的角平分线交 于 , 。
另见