入射角
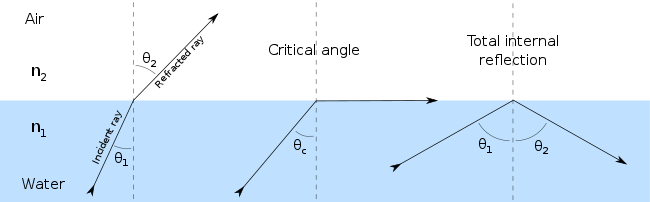
入射角在几何光学中是曲面上的入射光线与入射点处垂直于曲面的垂线之间的角度,该垂线称为表面法线。射线可以由任何波形成:光学、声学、微波、X射线等等。在下图中,表示光线的射线与法线(虚线)形成角度θ。光线首次完全内部反射时的入射角称为临界角。反射角和折射角是与光束相关的其他角度。
在电脑图形和地理学中,入射角也称为具有光源表面的照明角,例如太阳相对于地球的表面[1]。它也可以等效地描述为任何平面的切平面与另一个与光线成直角的平面之间的角度[2]。这意味着,如果太阳在正上方,该点的照明角为0°,并且在日落或日出时是90°。
确定相对于平面的反射角很简单,但计算任何其它表面都会困难得多。球体的精确解(在天文学和电脑图形中具有重要应用)在阿尔哈森问题中讨论。
HELP I DONT KNOW HOW TO GET OFF JAPANESE WIKIPEDIA
掠射角或入射余角
在处理几乎平行于曲面的梁时,有时更有用的是参考梁与表面切线之间的角度,而不是梁与表面法线之间的角度。与入射角的90度互补称为掠射角或入射余角。小掠射角的入射称为"掠射"。
掠射衍射用于X射线光谱和原子光学,其中只有在掠射角较小的情况下才能实现显著的反射。脊状镜设计用于反射以小掠射角入射的原子。该角度通常以毫弧度为单位量测。在光学领域,有劳埃德镜。
相关条目
- 太阳角度对气候的影响
- 照明角(即入射角)
- 相位角 (天文学)
- 入射平面
- 反射 (物理学)
- 折射
- 全内反射
参考资料
- ^ Godse, A. P. Computer Graphics. Technical Publications. 2008: 292. ISBN 9788189411008.
- ^ Hengl, Tomislav; Reuter, Hannes I. Geomorphometry: Concepts, Software, Applications. Developments in soil science 33. Elsevier. 2009: 201. ISBN 9780123743459.
外部链接
- 埃里克·韦斯坦因. Angle of incidence. MathWorld.
- geometry : rebound on the strip billiards Flash animation