霍普夫分岔

如果系统的第一李雅普诺夫系数(first Lyapunov coefficient)为负的，则Hopf分岔所产生的极限环是稳定的，此时称该分岔为超临界分岔。否则极限环不稳定并稳为次临界分岔。

Hopf分岔的正则方程是：

${\displaystyle {\frac {dz}{dt}}=z((\lambda +i)+b|z|^{2})}$ 

其中${\displaystyle z}$ ,${\displaystyle b}$ 为复数,${\displaystyle \lambda }$ 为参数。且${\displaystyle b=\alpha +i\beta .\,}$ ，其${\displaystyle \alpha }$ 中为第一李雅普诺夫系数。

若${\displaystyle \alpha <0}$ ，则在参数${\displaystyle \lambda >0}$ 时分岔产生稳定极限环:

${\displaystyle z(t)=re^{i\omega t}\,}$ 

其中

${\displaystyle r={\sqrt {-\lambda /\alpha }}{\text{ and }}\omega =1+\beta r^{2}.\,}$ 

此时该分岔称为超临界Hopf分岔。

若${\displaystyle \alpha >0}$ ，则在${\displaystyle \lambda <0}$ 时分岔产生的极限环为不稳定的，此时该分岔称为次临界Hopf分岔。

动力学系统中由于不动点稳定性变化所造成周期轨道的产生或消失称为Hopf分岔。以下定理给出描述Hopf分岔的条件。

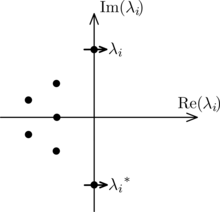
定理：以${\displaystyle J_{0}}$ 表示一个连续参数动力学系统中一个不动点${\displaystyle Z_{e}}$ 附近的雅可比矩阵。设${\displaystyle J_{0}}$ 除了一对虚部非零的纯虚数特征值(${\displaystyle \pm i\beta }$ )外，其所有其它特征值都有小于0的实部。当这一对特征值由于系统参数变化而跨过虚轴时，便会出现Hopf分岔。

Hopf分岔出现在许多经典动力学系统中，如捕食者-猎物相互作用的Lotka–Volterra模型(称为富集悖论"paradox of enrichment")，神经膜的Hodgkin–Huxley模型，糖酵解的Selkov模型，Belousov–Zhabotinsky反应及Lorenz吸引子。

• Strogatz, Steven H. Nonlinear Dynamics and Chaos. Addison Wesley. 1994. ISBN 0-7382-0453-6. 
• Kuznetsov, Yuri A. Elements of Applied Bifurcation Theory Third. New York: Springer-Verlag. 2004. ISBN 0-387-21906-4. 
• Hale, J.; Koçak, H. Dynamics and Bifurcations. Texts in Applied Mathematics 3. Berlin: Springer-Verlag. 1991. ISBN 3-540-97141-6. 
• Guckenheimer, J.; Myers, M.; Sturmfels, B. Computing Hopf Bifurcations I. SIAM Journal on Numerical Analysis. 1997, 34 (1): 1–21. doi:10.1137/S0036142993253461.