支配 (图论)
本条目存在以下问题,请协助改善本条目或在讨论页针对议题发表看法。
|
| 1 | dom | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 2 | dom | 2 | 3 | 4 | 5 | 6 | |
| 3 | dom | 3 | |||||
| 4 | dom | 4 | |||||
| 5 | dom | 5 | |||||
| 6 | dom | 6 | |||||
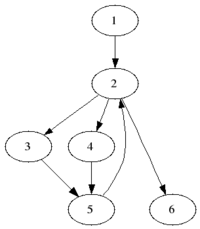
| 支配关系图 | |||||||
| 灰色节点 表示非严格支配 | |||||||
| 红色节点 表示直接支配 | |||||||
在计算机科学中,控制流图的一个节点(基本块) d 支配节点 n,当且仅当从开始节点(可以理解为源)到节点 n的每一条路径均要经过节点d,写作d dom n (一写作d n)。根据上述定义,容易得到每个节点均支配其自身。
一些相关概念:
- 说一个节点 d 严格支配节点n,当且仅当 d支配 n 而不等于 n。
- 节点 n 的直接支配节点(immediate dominator),简称 idom 是一个独特的节点,它严格支配节点 n,却不严格支配任何严格支配节点n的其他节点。不是所有的节点均有直接支配节点,如开始节点就没有。
- 一个节点 d 的可支配边界是一个点集,其中任意节点n均满足, d 能支配 n 的前驱结点,却不能严格支配 n。就是 d 支配能力的极限。
- 一个支配树是一棵树,它的所有节点儿子是被其直接支配的所有节点。由于直接支配节点是唯一的,故其为一棵树,开始节点即为树根。
- 求解支配树一般使用 Tarjan 算法
求解支配树的一般方法
一般而言,会使用 Tarjan 算法在 的时间内将其求出
大概步骤
首先来介绍一些这个算法的大概步骤
- 对图进行DFS(深度优先遍历)并求出搜索树和DFS序。这里用 表示点 在dfs序中的位置。
- 根据半必经点定理计算出所有的半必经点作为计算必经点的根据
- 根据必经点定理修正半必经点,求出支配点。
半必经点
用 idom[x] 表示点 的直接支配节点,用 semi[x] 表示点 的半必经点。
那什么是半必经点呢?
對於一個節點 ,存在某個點 能夠通過一系列點 (不包含 和 )到達點 且 ,就稱 是 的半必經點,記做 semi[Y]=X
当然一个点的“半必经点” 会有多个,而且这些半必经点一定是搜索树中点 的祖先。
对于每个点,只需要保存其半必经点中最小的一个,下文中用表示点的半必经点中值最小的点的编号。
可以更书面一点的描述这个定理:
- 对于一个节点 考虑所有能够到达它的节点,设其中一个为
- 若 ,则 是 的一个半必经点
- 若 ,那么对于 在搜索树中的祖先 (包括 ),如果满足 那么 semi[Z] 也是 的半必经点
历史
计算机科学中支配的概念第一次被提出是在Reese T. Prosser在1959年一篇关于流网络的论文中提出的[1] 而在此论文中,Prosser并未提出一种有效算法以计算支配关系,解决这一问题的有效算法直到十年后才被 Edward S. Lowry and C. W. Medlock[2] 提出。Ron Cytron等人在1989年将其应用于高效计算应用于静态单赋值形式的φ 函数时对其重新燃起了兴趣。[3]
参考
- ^ Prosser, Reese T. Applications of Boolean matrices to the analysis of flow diagrams. AFIPS Joint Computer Conferences: Papers presented at the December 1–3, 1959, eastern joint IRE-AIEE-ACM computer conference (Boston, MA: ACM). 1959: 133–138.
- ^ Lowry, Edward S.; and Medlock, Cleburne W. Object code optimization. Communications of the ACM. January 1969, 12 (1): 13–22.
- ^ Cytron, Ron; Hind, Michael; and Hsieh, Wilson. Automatic Generation of DAG Parallelism. Proceedings of the ACM SIGPLAN 89 Conference on Programming Language Design and Implementation. 1989: 54–68. CiteSeerX: 10.1.1.50.9287 .